Расчет годовых процентов: формула, правила расчета и примеры расчетов

Сложный процент. Формулы расчета сложного процента

Люди во все времена думали о своем завтрашнем дне. Они старались и стараются обезопасить от финансовых невзгод и себя, и своих детей и внуков, строя хотя бы небольшой островок уверенности в будущем. Начиная строить его уже сейчас с помощью небольших банковских вкладов, можно обеспечить себе в дальнейшем стабильность и независимость.

Основным принципом банковских операций является то, что денежные средства способны увеличиваться лишь тогда, когда находятся в постоянном обороте. Чтобы клиентам уверенно ориентироваться в сфере финансовых услуг и уметь правильно подбирать условия, выгодные им в определенный промежуток времени, необходимо знать ряд простых правил. В данной статье речь пойдет о долгосрочных вложениях, которые позволяют за определенное количество лет из относительно небольшой суммы начального капитала получить существенную прибыль или использовать вклад дальше, снимая начисления для повседневных нужд.

Для правильного расчета прибыли необходимо выполнить несложные арифметические действия на основе нижеизложенных формул.

Формула сложного процента (расчет в годах)

Например, вы решили положить 100000,00 руб. под 11% годовых, чтобы через 10 лет воспользоваться сбережениями, которые значительно выросли в результате капитализации. Для расчета итоговой суммы следует применить методику расчета сложного процента.

Применение сложного процента подразумевает то, что в конце каждого периода (год, квартал, месяц) начисленная прибыль суммируется с вкладом. Полученная сумма является базисом для последующего увеличения прибыли.

Для расчета сложного процента применяем простую формулу:

где

• S – общая сумма («тело» вклада + проценты), причитающаяся к возврату вкладчику по истечении срока действия вклада;
• Р – первоначальная величина вклада;
• n — общее количество операций по капитализации процентов за весь срок привлечения денежных средств (в данном случае оно соответствует количеству лет);
• I – годовая процентная ставка.

Подставив значения в эту формулу, мы видим, что:

через 5 лет сумма будет равняться 168505,81 рублей:

а через 10 лет она составит  283942,09 рублей :

Если бы мы рассчитывали капитализацию процентов по вкладу за короткий период, то сложный процент было бы удобнее рассчитывать по формуле

где:

• К – количество дней в текущем году,
• J – количество дней в периоде, по итогам которого банком производится капитализация начисленных процентов (остальные обозначения – как и в предыдущей формуле).

Но тем, кому удобнее ежемесячно снимать проценты по вкладу, лучше ознакомиться с понятием «капитализация вклада», подразумевающим начисление простых процентов.

На графике показано как вырастет капитал при капитализации процентов по вкладу, если вложить 100000,00 руб. на 10 лет под 10%, 15% и 20%

Формула сложного процента (расчет в месяцах)

Существует и другой, более выгодный для клиента метод начисления и прибавления процентной ставки – ежемесячный. Для этого применяется следующая формула:

где n также соответствует количеству операций по капитализации, но уже выражается в месяцах. Процентный показатель здесь дополнительно делится на 12 потому что в году 12 месяцев, а у нас появляется необходимость в расчете месячную процентную ставку.

Если бы данная формула использовалась для поквартального начисления вклада, то годовой процент делился бы на 4, а показатель n был бы равен количеству кварталов, а если бы процент начислялся по полугодиям, то процентная ставка делилась бы 2, а обозначение n соответствовало количеству полугодий.

Итак, если бы нами был сделан вклад в сумме 100000,00 руб. с ежемесячной капитализацией процентов, то:

через 5 лет (60 месяцев) сумма вклада выросла бы до 172891,57 руб., что примерно на 10000 руб. больше, чем в случае с ежегодной капитализацией вклада;руб.

а через 10 лет (120 месяцев) «наращенная» сумма составила бы 298914,96 руб., что уже на целых 15000 руб. превосходит показатель, рассчитанный по формуле сложного процента, предусматривающей расчет в годах.

Это означает, что доходность при ежемесячном начислении процентов оказывается больше, чем при начислении один раз в год. И если прибыль не снимать, то сложный процент работает на пользу вкладчика.

График, показывающий разницу роста капитала при расчете в годах и при ежемесячной капитализации процентов

По данным с http://101.credit/articles/vkladi/clozhnyjj-procent/

Обратное вычисление

Очень часто в вопросе о том, как посчитать процент от суммы, возникает и недвусмысленный обратный перевод. На практике это связано, скажем, с обратным вычислением четверти. Всем известно, что этот показатель составляет 25% от начального числа. Пусть, например, цену товара увеличили на 25%, что составило 25 рублей. Нужно найти, сколько стал стоить данный товар. Вот теперь попробуем разобраться, как вычислить не первоначальное число, зная значение процента, а всю сумму, которая должна получиться в конечном итоге. Казалось бы, решение простое:

25 = 25% (1/4 или 0,25);

Нет, абсолютно неверно. Так можно получить только изначальное число, без учета 25%. Для расчета всей суммы с учетом 25% нужно использовать формулу:

Или 100/0,8, что и покажет значение 125 (100 + 25), поскольку 100% плюс 25% в выражении единицы является числом 1,25 (единица плюс четвертая часть), а в обратном виде (1/x) – это именно 0,8. Произведя вычисления, получим, что х = 125.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

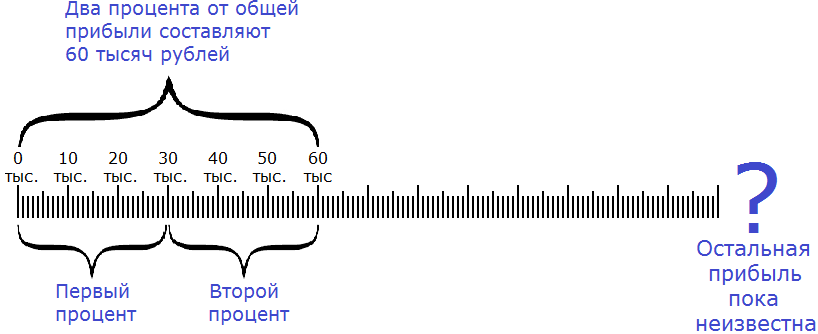
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Расчет с помощью формул

Итак, рассмотрим некоторые формулы для расчета. Формула вычисления процента от определенного значения.

Если известно число А и составляющее от процента В, то процент от А находится так:

Есть специальная формула для вычисления по проценту. При этом нужно узнать от какого значения %.

Если известно В, которое составляет Р процентов от числа А, то количество А находится так. А=В*100%/Р. Можно также вычислить процентное значение одного числа от другого. Если известны два значения А и В, то можно выяснить, какой % содержит В от А. При этом применяется такая формула. Р=В/А*100%. Чтобы узнать насколько увеличилось число по сравнению с исходным, также есть определенная формула.

Если известно число А и необходимо найти В, которое на определенный процент больше числа А, то применяется такая формула: В=А(1+Р/100%) . Также есть формула для расчетов, которое меньше исходного на какой-то заданный процент.

Если мы знаем число А и необходимо отыскать В, которое на Р % меньше А, то применяется такое вычисление: В=А(1-Р/100%).

Вспоминайте школьные знания и используйте их в обычной жизни. Математические расчеты здорово упрощают жизнь.

На сегодня у меня все. До свидания, дорогие почитатели моего блога!

Правила записи чисел, имеющих дробную часть, предусматривают несколько форматов, основными из которых являются «десятичный» и «обыкновенный». Обыкновенные дроби, в свою очередь, могут быть записаны в форматах, называемых «неправильными» и «смешанными». Для выделения целой части из дробного числа каждого из этих вариантов записи удобнее применять различающиеся способы.

Отбросьте дробную часть, если надо выделить из положительной дроби, записанной в смешанном формате. В такой дроби целая часть перед дробной – например, 12 ⅔. В этой дроби целой частью будет число 12. Если смешанная дробь имеет знак, то полученное таким способом число уменьшайте на единицу. Необходимость этого действия вытекает из определения целой части числа, согласно она не может быть больше значения исходной дроби. Например, целой частью дроби -12 ⅔ является число -13.

Разделите без остатка числитель исходной дроби на ее знаменатель, если она записана в неправильном обыкновенном формате. Если исходное число имеет положительный знак, то полученный результат и будет целой частью. Например, целая часть дроби 716/51 равна 14. Если же исходное число отрицательно, то и здесь от результата следует отнять единицу – например, вычисление целой части дроби -716/51 должно дать число -15.

Считайте ноль целой частью положительной дроби, записанной в обыкновенном формате и при этом не являющейся ни смешанной, ни неправильной. Например, это к дроби 48/51. Если исходная дробь меньше нуля, то, как и в предыдущих случаях, результат нужно на один. Например, целой частью дроби -48/51 следует считать число -1.

Отбросьте все знаки, стоящие после десятичной запятой, если выделить надо из положительного числа, записанного в формате десятичной дроби. В этом случае именно разделительная

Практические навыки

ТР. показывает, сколько процентов составляет одно число от другого. С помощью ТП можно вычислить, на сколько процентов возросло или сократилось число относительно другого.

Использование формул

ТР не бывает отрицательным, а ТП может. ТП определяется на базе ТР, обратный порядок недопустим. Чтобы высчитать величину, применяется ПП, поскольку он наглядно отражает динамику изменений.

Можно на примере посчитать темп роста в процентах. Работник завода получал заработную плату каждый месяц в зависимости от выработки. В январе сотрудник получил 40000 рублей, в феврале 45000 р. ТР составляет по формуле: 45000/40000*100 = 112,5. Таким образом, в феврале доход относительно предыдущего месяца может исчисляться как 112%.

Формулы широко применяются в повседневной жизни населения. В интернете имеется онлайн-калькулятор, позволяющий получить реальный результат или проверить собственные решения. Их использование позволяет опустить ошибки расчетов.

Разные методы расчета

Наглядное использование формул на примере позволит проанализировать предназначение ТР и ТП. В таблице представлен внутренний валовой продукт России с 2010—2017 годы. Необходимо найти ТР (в процентах) базисным и цепным методами.

Таблица данных о ВВП в национальной валюте за 2011−2018 гг.

Период	ВВП России ТР	(%)
в млрд р.	Цепной метод	Базисный метод
2011	48 000	–	–
2012	57 698	120,2	120,2
2013	66 817	115,8	139,2
2014	71 117	106,4	148,2
2015	78 945	111,0	164,5
2016	80 826	102,4	168,4
2017	83 871	103,8	174,7
2018	88 177	105,1	183,7

Формула цепного метода: ТР= Yi / Yi -1*100.

Для 2011 величины не будет. Начиная с 2012 года: 57698/48000*100 = 120,2%. Для 2013 года: 66817/57698*100 = 115,8%. Таким способом высчитываются суммы для каждого периода.

Базисный метод: ТР = Yi/Ybasic*100. Это отношение к основному, первому коэффициенту. Например, для 2012 года суммы высчитываются 57698/48000*100 = 120,2%, для 2013 года: 66817/48000*100 = 115,8%. Таким принципом вычисляются все оставшиеся периоды.

Таким же способом рассчитывается процентное соотношение данных актива баланса, отчета о прибылях и убытках. Показатели, отражающие величину чистой прибыли за 2 года, позволят выявить прирост или снижение показателей.

Данные	2017	2018	ТР %
Выручка от реализации	1500000	1600000	106,7
Финансовые доходы	400000	350000	87,5

За 2018 год ТР составит 106,7% выручки, а доходы от вложений возросли на 87,5%.

ТР необходим, чтобы узнать, сколько процентов составляет одно значение от другого. Последним выступает предыдущее число. Темп прироста позволяет выяснить, насколько изменился заданный параметр.

На основе одного из коэффициентов нельзя составить верную оценку определяемому явлению (по международному, отечественному рынку, предприятию, показателю работоспособности фирмы). Необходимы комплексные меры изучения и расчетов показателей в динамике. Для анализа финансовой деятельности можно брать разную информацию из форм отчетности.

Как рассчитать через Excel?

Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 36 месяцев, нужно составить таблицу, в которую внести 5 столбиков:

1 – сверху вниз указываются месяцы от 1 до 36;

2 — (В4) вписывается в строку сумма вклада – 50 000 руб.;

3 – (С4) указывается % — 8;

4 – (D4) вставляется формула для расчета ежемесячных %: =B4*$C$4/12, в которой В4 – сумма вклада, С4 -% (нужно проставлять значок $, чтобы формула выбирала данное поле, или путем выделения графы С4 курсором с нажатием клавиши F4 на клавиатуре), 12 – месяцы (% высчитывается в годовых);

5 – (Е4) считается новая сумма вклада, которая будет использована для начисления процента. Нужно написать формулу =B4+D4, в которой В4 – сумма вклада, D4 – сумма %, которые были начислены. Это будет новая сумма вклада, исходя из которой начисляются %.

В графу В5 заносится формула = Е4, в которой Е4 – это сумма вклада на истекший месяц с процентами.

Далее нужно скопировать формулы:

• подвести курсор к углу ячейки В5, он изменится с белого плюса на черный;
• потянуть его вниз, произойдет автоматическое копирование формулы из этой ячейки в другие;
• эту же операцию нужно выполнить с формулами, вписанными в ячейки D4, E4.
• В итоге, если все выполнено правильно, должен получиться ответ 63 512 руб.

Как рассчитать процент от суммы

Очень часто приходится сталкиваться с несколькими искомыми числами или их суммой. Вопрос о том, как расчитывать проценты от суммы, решается так же просто, как и в случае использования одного начального числа. Единственное, что нужно учесть в этом случае, так это обычное представление суммы в виде единого значения.

Например, у нас имеется два числа, a и b, и начальным показателем выступает число d. В данном случае пропорция будет выглядеть следующим образом:

Заметьте, сумму (a + b) все равно можно представить в виде единого числа. Пускай это будет z. В случае, когда мы задаем формулу a + b = z, пропорция приобретает совершенно стандартный вид:

Как видим, ничего сложного в этом нет.

Есть и другой вариант, когда сумма (a + b) = 100%, а d = x.

Тут решение выглядит так:

(d x 100)/(a + b) или (d/(a + b)) + 100/(a + b).

Как уже понятно, здесь используется принцип общего знаменателя для дробей.

Если сложить a и b, сумма которых равна z, то пропорция опять возвращается к стандартному виду:

То же применяется и в обратном порядке.

Данные для расчетов

Чтобы правильно рассчитать процентную ставку и величину переплаты, необходимо знать точную информацию о планируемом к оформлению кредите

Важно понимать, по какой схеме будет погашаться долг: аннуитетной или дифференцированной. Это поможет выбрать формулу для вычислений

Кроме этого необходимо знать:

• сумму кредита;
• размер годовой ставки;
• период погашения займа.

Указанные нюансы всегда учитываются в калькуляторах, представленных на сайтах банков. Поэтому, зная все параметры ссуды, можно максимально точно подсчитать переплату по кредиту. Разберемся, что за формулу нужно применять при аннуитете и дифференциале.

Работа с процентами в Excel

Посчитать процент от числа, прибавить, отнять проценты на современном калькуляторе не составит труда. Главное условие – на клавиатуре должен быть соответствующий значок (%). А дальше – дело техники и внимательности.

Например, 25 + 5%. Чтобы найти значение выражения, нужно набрать на калькуляторе данную последовательность цифр и знаков. Результат – 26,25. Большого ума с такой техникой не нужно.

Для составления формул в Excel вспомним школьные азы:

Процент – сотая часть целого.

Чтобы найти процент от целого числа, необходимо разделить искомую долю на целое и итог умножить на 100.

Пример. Привезли 30 единиц товара. В первый день продали 5 единиц. Сколько процентов товара реализовали?

5 – это часть. 30 – целое. Подставляем данные в формулу:

(5/30) * 100 = 16,7%

Чтобы прибавить процент к числу в Excel (25 + 5%), нужно сначала найти 5% от 25. В школе составляли пропорцию:

25 – 100%;

х – 5%.

Х = (25 * 5) /100 = 1,25

После этого можно выполнять сложение.

Когда базовые вычислительные умения восстановлены, с формулами разобраться будет несложно.

Что такое процент?

Проце́нт (лат. per cent — на сотню) — одна сотая часть. Отмечается знаком «%». Обозначает долю чего-либо по отношению к целому. Например, 25 % от 500 руб. означает 25 частей по 5 руб. каждая, то есть 125 руб.

Базовая формула расчета процента от суммы выглядит так:

Не существует универсальной формулы, подходящей для каждого сценария расчета процентов. Ниже вы узнаете о самых популярных способах расчета.

Видео урок:

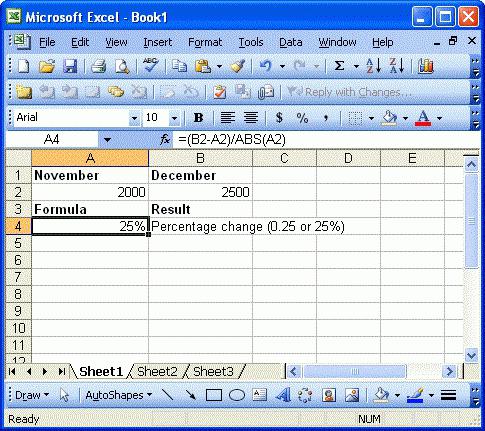
Но если использовать формат ячейки “Процентный”, то для вычисления процента от числа достаточно поделить одно число на другое. Например, у нас есть яблоки, которые мы купили по 100 руб. на оптовом складе, а розничную цену выставим 150 руб. Для того чтобы высчитать процент того, сколько составляет закупочная цена от розничной, нам потребуется:

Составить таблицу с ценами и добавить колонку для вычисления величины процента:

В ячейку D2 внести формулу, вычисляющую процент цены закупки от цены продажи:

Видеоурок:

Представим, что у нас есть список продавцов с объемом продаж по каждому и общей суммой всех продаж по всем продавцам. Наша задача определить, какой процент составляет вклад каждого продавца в итоговый оборот:

Для этого нам нужно:

• Добавить колонку к таблице с расчетом процента;
• В ячейку C2 вставить формулу:

Значки $ фиксируют колонку “B” и ячейку “9” для того, чтобы при протягивании формулы на все строки таблицы, Excel автоматически подставлял объем продаж каждого продавца и высчитывал % от общего объема продаж. Если не поставить значки “$”, то при протягивании формулы, система будет смещать ячейку B9 на столько ячеек вниз, на сколько вы протяните формулу.

Протянуть формулу на все ячейки таблицы, соответствующие строкам с фамилиями продавцов:

На примере выше мы протянули формулу и получили значения в виде дробных чисел. Для того чтобы перевести полученные данные в проценты выделите данные левой клавишей мыши и смените формат ячеек на “Процентный”:

Видеоурок:

На примере выше у нас был список продавцов и их объем продаж. Мы вычисляли какой вклад каждый из работников внес в итоговый объем продаж. Но что, если у нас есть список повторяющихся товаров с данными объема продаж и нам нужно вычислить какую часть конкретный товар составляет в процентах от всех продаж?

Из списка товаров выше мы хотим вычислить какой объем продаж составляют помидоры (они записаны в нескольких строках таблицы). Для этого:

Справа от таблицы укажем товар (Помидоры), по которым хотим рассчитать долю в продажах:

• Сменим формат ячейки E2 на “Процентный”;
• В ячейку E2 вставим формулу с функцией СУММЕСЛИ, которая поможет вычислить из списка товаров Помидоры и суммировать их объем продаж, а затем поделить его на общий объем продаж товаров:

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

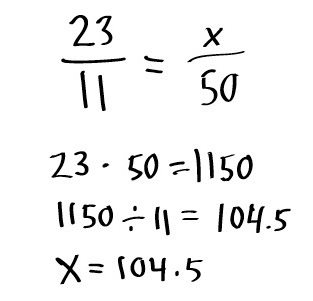
В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») – в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Быстрое вычисление процентов

Конечно, вычисление процентов при помощи пропорции является фундаментальным. Однако с применением дробных чисел это процедура упрощается до невозможности. Ведь что такое 50% на самом деле? Половина. То есть 1/2 или 0,5 (исходя из начального числа 1). Теперь понятно: чтобы вычислить половину, нужно умножить искомое число или на 1/2, или на 0,5 либо разделить на 2. Такой способ, правда, годится только для чисел, которые делятся без остатка.

В случае возникновения остатка или бесконечных знаков в периоде после запятой типа 0,33333333… лучше использовать дробные выражения наподобие 1/3. Кстати, именно дроби (в некоторых случаях иррациональные) со всей точностью отражают само число, ведь периодические цифры после запятой, сколько ни задавай, все равно целого числа не дадут. А так та же одна треть четко и понятно выражает саму суть.

В тех же рецептах, естественно, треть можно определить, так сказать, на глаз. А вот в химических процессах, особенно связанных с тонкой дозировкой компонентов, скажем, в фармацевтике, такой метод не подойдет. Здесь на глаз полагаться не приходится. Необходимо использовать точные соотношения ингредиентов, даже если один из показателей имеет вид числа с цифрой в периоде или представлен в виде той же иррациональной дроби. Но, как правило, к примеру при взвешивании, такие числа могут ограничиваться после запятой десятитысячными или максимум стотысячными.

Формула сложных процентов.

Она применяется реже в депозитной практике банка, но такие предложения найти можно. Для большинства вкладчиков они  не являются привлекательными по причине того, что ставки по ним ниже, чем по продуктам, когда доход начисляется  только по окончании действия депозитного договора. Периодичность присоединения дохода может быть разной: раз в месяц, раз в неделю, раз в квартал, каждый год. Она подразумевает под собой капитализацию или начисление «процентов на проценты».

Формула сложных %-ов:

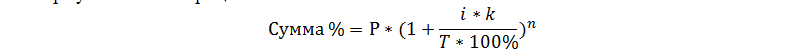
P – изначальная сумма вклада.

i – депозитная годовая ставка.

k – число дней в периоде, через который начисляется доход.

T – число дней в году.

n – число капитализаций дохода в течение всего срока депозита.

Рассмотрим пример №1: разместим 100 000 рублей под 12% годовых на полгода с ежемесячной капитализацией.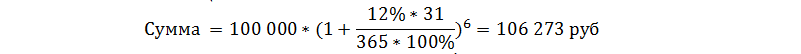
Полученное значение подтвердим через расчеты в Excel.

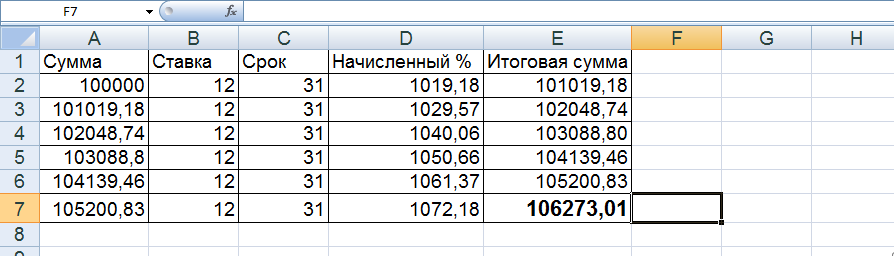
Таким образом, благодаря ежемесячной капитализации, общий итог вложений оказался выгоднее, чем в варианте, когда проценты причисляются  в конце срока.

Пример №2: разместим 100 000 рублей на 6 месяцев под 12% годовых с еженедельной капитализацией.

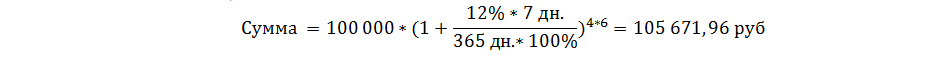
Полученное значение подтвердим через расчеты в Excel.

Пример №3: разместим 100 000 рублей на 1 год под 12% годовых с ежеквартальной капитализацией.

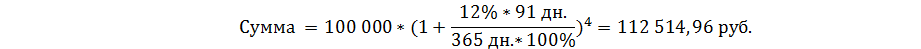
Полученное значение подтвердим через расчеты в Excel.

Пример №4: разместим 100 000 руб на 1 месяц под 12% годовых с ежедневной капитализацией.

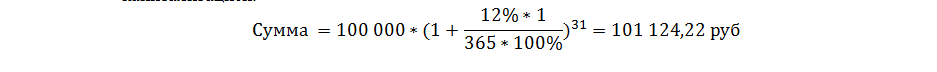
Полученное значение подтвердим через расчеты в Excel.

Таким образом, капитализация и формула сложных процентов дает более выгодный эффект, поэтому, при размещении денег в банке не стоит упускать из виду подобные варианты размещения.

Бесполезно
24

Занятно
20

Помогло
35

Расчет процентов

Для начисления процентной ставки банки используют два метода: аннуитетный и дифференцированный. Основное отличие каждого из методов в скорости выплаты процентов по кредиту.

Дифференцированные платежи предполагают уплату ежемесячного платежа в разной сумме на протяжении всего срока действия кредитного договора, при котором в первую очередь выплачиваются проценты банку, а ближе к концу кредитного соглашения погашается основная сумма задолженности. Стоит отметить, что проценты насчитываются каждый раз на остаток кредитного долга. Для расчета такого способа оплаты кредита используют формулу:

Сумма платежа = остаток по займу*% по кредиту*количество дней/100/365

Как вычесть проценты в заполненной таблице

Часто случаются ситуации, когда в таблицу уже занесены данные, и нужно выполнить расчет процентов из определенных числовых значений. Для того чтобы сделать это вручную, понадобится большое количество времени, есть высокий шанс допустить ошибку или изменить какие-либо другие показатели в самой таблице. Есть другой более автоматизированный и точный способ, который состоит из нескольких действий:

1. Для получения процента от числовых значений в клетках одного столбца необходимо левой кнопкой мыши отметить свободную ячейку рядом с начальной клеткой данного столбца.
2. Прописать символ «=».
3. Нажать на ту клетку рядом с записанным числовым значением.
4. Написать символ «-».
5. Нажать на ту же ячейку еще раз, чтобы ее координаты повторно занеслись в клетку.
6. Завершить формулу требуемым числом процентов, написать знак «%».

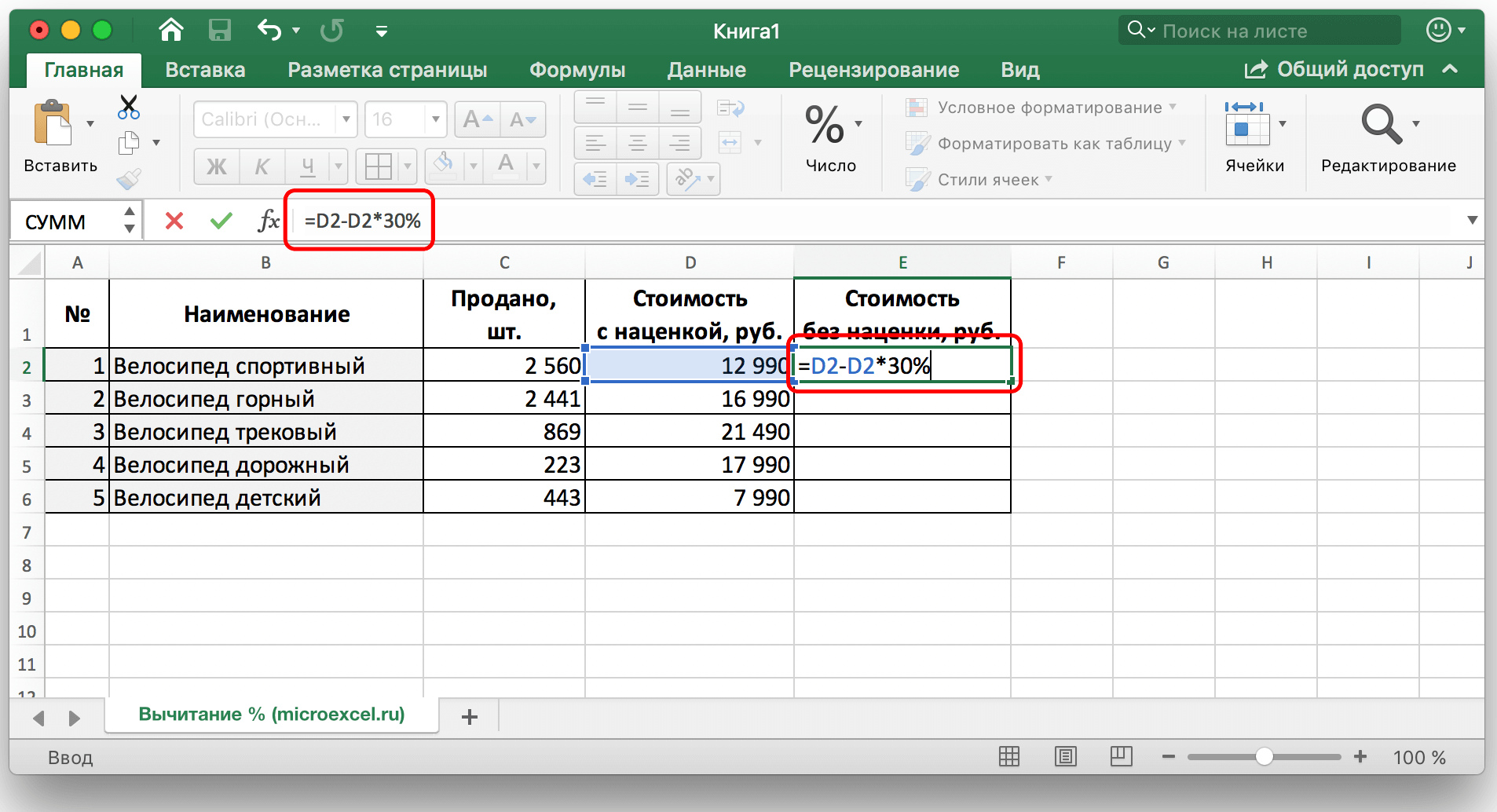Расчет процента от определенных числовых значений в готовой таблице

В итоге должен получиться требуемый результат. Однако в процессе подобного расчета процент будет получен только к одному числовому значению из таблицы. Чтобы автоматизировать его для других клеток, необходимо выполнить еще несколько дополнительных действий:

1. Выделить нажатием ЛКМ ячейку с готовым результатом.
2. Направить курсор на край ячейки, чтобы в правом нижнем углу появилось изображение черного крестика.
3. Зажать левой кнопкой мыши крестик, растянуть курсор на нужное количество ячеек вниз.

После этого в соседнем столбце должны появиться результаты заданных расчетов.

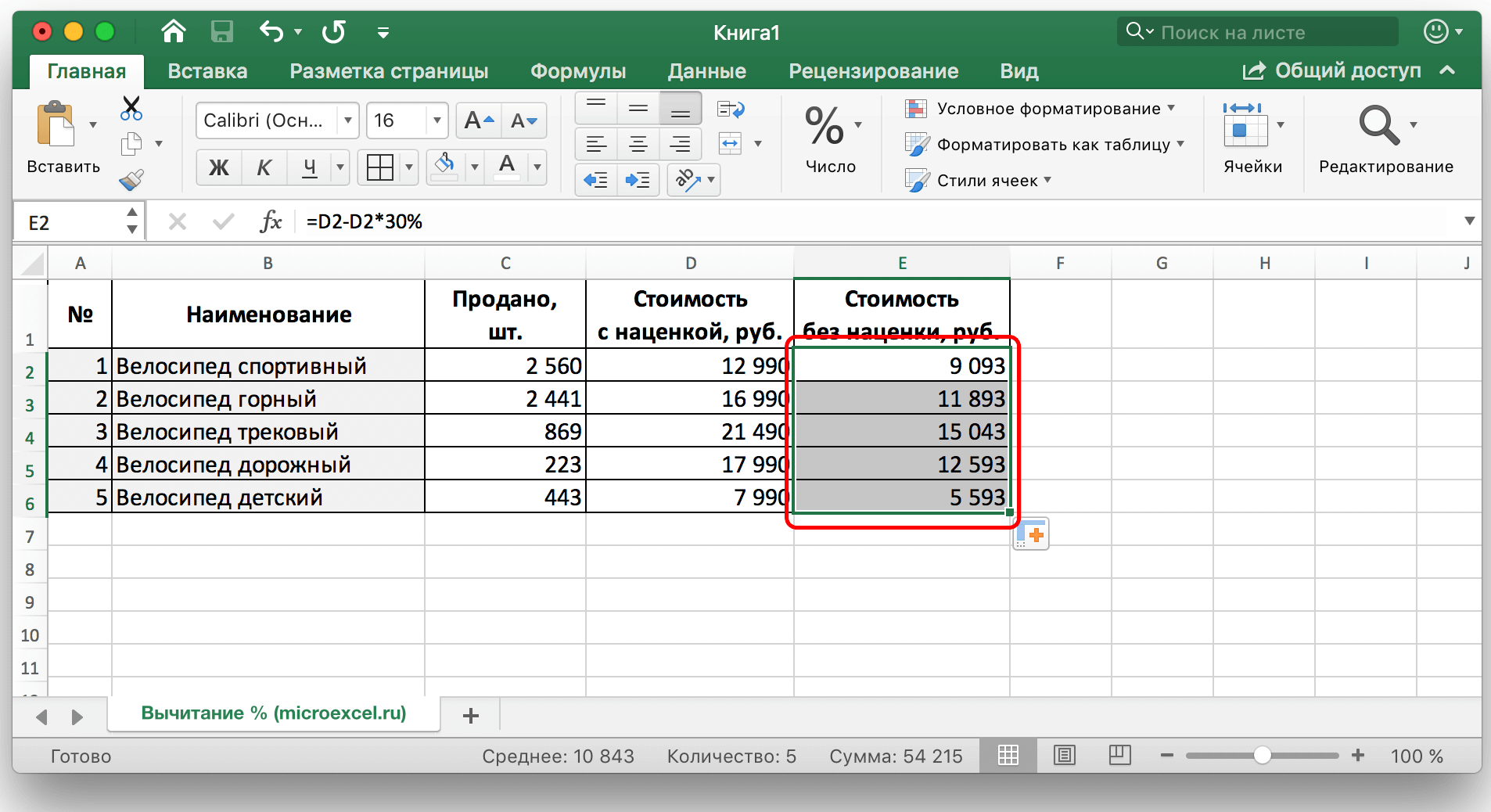Автоматизации процесса вычисления процентов для каждой из ячеек одного столбца