Math.random()

Генерирование целочисленных псевдослучайных значений

Для генерирования целочисленных псевдослучайных значений используется представленное выше выражение, в котором
произведение «приводится» к целочисленному значению. Например, попробуем получить псевдослучайное значение в диапазоне

Обратите внимание, что закрывающаяся скобка квадратная, т.е. 20 входит в диапазон

В этом случае к разности
между максимальным и минимальным значениями следует добавить 1, т.е. определить диапазон целочисленных значений [5,21),
где 21 не попадает в желаемый диапазон :

// после подстановки значений
int i = (int)Math.random() * (20 - 5 + 1) + 5;
// получаем
int i = (int)Math.random() * 16 + 5;

Other Pseudo-Random Number Generators

Crypto.getRandomValues()

Cryptographically strong pseudo-random values are available on all web browsers that support . Implementations vary across user agents, but all are required to use a seed with enough entropy. To fill an array with results try:

The Middle Square Method

Invented by John von Neumann around 1946, the Middle Square Method (MSM) generates a pseudo-random number sequence by extracting the middle digits from a squared number.

Beware of certain seed values, like 25, which have a shorter cycle or cause the algorithm to repeat one value indefinitely.

Linear Congruential Generator

Invented around 1958 by Thomson & Rotenberg, the Linear Congruential Generator (LGC) algorithm is perhaps the oldest-known. It’s fast, and when care is taken with the initial values, quite adequate.

Xorshift family of pseudo-random number generators

Xorshift or “shift-register generators” are a family of pseudorandom number generators that were discovered by George Marsaglia in 2003. Among the fastest PRNGs, they use bitwise operations to deliver a high-quality sequence.

The xorshift variants —  xorwow, xorshift+, xoshiro, xoroshiro, xoshiro256*, xoshiro256+ — each provide a different method; research into the suitability of each of these for your needs is time well spent.

Что такое генераторы псевдослучайных чисел?

Эта иллюстрация поясняет мысль фон Неймана: очевидно, что сгенерированная последовательность чисел не является случайной. Для многих задач этого вполне достаточно. Но нам нужен алгоритм, генерирующий числа, которые кажутся случайными. Технически они должны казаться независимыми и одинаково распределёнными случайными переменными, равномерно распределёнными по всему диапазону генератора. Другими словами, нам нужно безопасно притвориться, что наши псевдослучайные числа являются истинно случайными.

Если результат работы генератора очень трудно отличить от истинно случайной последовательности, то его называют высококачественным генератором. В противном случае — низкокачественным. По большей части качество определяется эмпирически, путём прогона статистических тестов на уровень случайности. Например, оценивается количество нулей и единиц, вычисляется число коллизий, применяется метод Монте-Карло для вычисления π и т. д. Другой, более прагматичный метод оценки качества PRNG заключается в анализе его работы на практике и сравнении с истинно случайными числами.

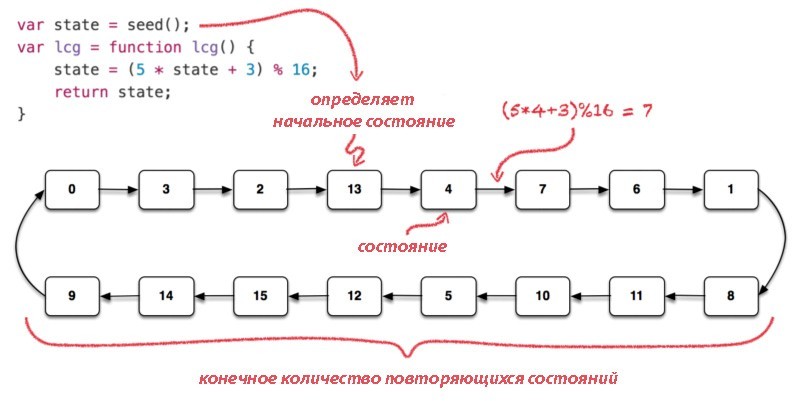
Помимо неслучайности результата, рассматриваемый нами простой алгоритм демонстрирует и другие важные особенности, свойственные всем PRNG. Если долго генерировать числа, то рано или поздно начнёт повторяться одна и та же последовательность. Это свойство называется периодичностью, и ею «страдают» все PRNG.

Период, или длина цикла, — это длина последовательности чисел, создаваемых генератором до первого повторения.

Можно рассматривать PRNG как сильно сжатую шифровальную книгу, содержащую последовательность чисел. Какой-нибудь шпион мог бы использовать его в качестве одноразового блокнота. Начальной позицией в этой «книге» является seed(). Постепенно вы дойдёте до её конца и вернётесь к началу, завершив цикл.

Большая длина цикла не гарантирует высокое качество, но весьма ему способствует. Часто он гарантируется каким-то математическим доказательством. Даже когда мы не можем точно вычислить длину цикла, нам вполне по силам определить его верхнюю границу. Поскольку следующее состояние PRNG и его результат являются детерминистическими функциями текущего состояния, то длина цикла не может быть больше количества возможных состояний. Для достижения максимальной длины генератор должен пройти через все возможные состояния, прежде чем вернуться в текущее.

Если состояние PRNG описывается как k-бит, то длина цикла ≤ 2k. Если она действительно достигает этого значения, то такой генератор называют генератором полного цикла. В хороших PRNG длина цикла близка к этой верхней границе. В противном случае вы будете зря тратить память.

Давайте теперь проанализируем количество уникальных случайных значений, генерируемых PRNG с помощью некой детерминистической трансформации выходных данных. Допустим, нам надо сгенерировать три случайных числа от 0 до 15, вроде 2, 13, 4 или 5, 12, 15. У нас может быть 163 = 4096 таких тройных комбинаций, но рассматриваемый нами простой генератор может выдать лишь 16 комбинаций:

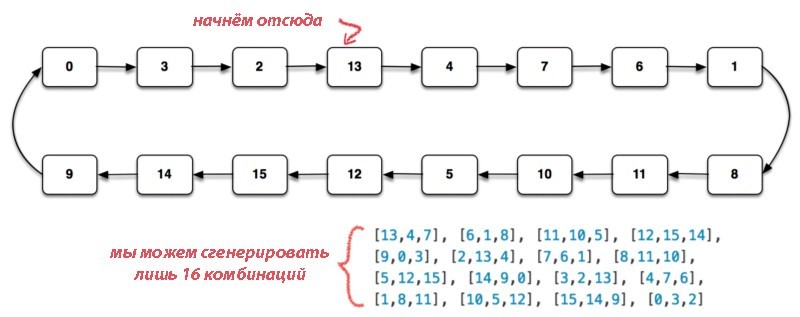
Так мы приходим к ещё одному свойству всех PRNG: количество уникальных значений, которые могут быть сгенерированы из псевдослучайной последовательности, ограничивается длиной цикла последовательности.

Неважно, какие значения мы генерируем в данном случае. Их может быть 16 комбинаций из четырёх значений (или любой другой длины), 16 уникальных матричных массивов и т

д. Не более 16 уникальных значений любого типа.

Вспомните наш алгоритм для генерирования случайных идентификаторов, состоящих из 22 символов, берущихся из 64-символьного словаря. Получается, что мы генерируем комбинации из 22 чисел от 0 до 63. И здесь мы сталкиваемся с той же проблемой: количество возможных уникальных идентификаторов ограничено размером внутреннего состояния PRNG и длиной его цикла.

What is Randomness in Javascript?

It is impossible in computing to generate completely random numbers. This is because every calculation inside a computer has a logical basis of cause and effect, while random events don’t follow that logic.

Computers are not capable of creating something truly random. True randomness is only possible through a source of external data that a computer cannot generate, such as the movement of many lava lamps at once (which has been used as an unbreakable random encryption in the real world), meteographic noise, or nuclear decay.

The solution that Javascript, and other programming languages, use to implement randomness is “pseudo-random” number generation. Javascript random numbers start from a hidden internal value called a “seed.” The seed is a starting point for a hidden sequence of numbers that are uniformly distributed throughout their possible range.

Developers cannot change Javascript’s pseudo-random seed or the distribution of values in its generated pseudo-random sequences. Different Javascript implementations and different browsers often start with different seeds. Do not assume that different browsers, or even different computers, will always use the same seed.

Javascript random numbers are not safe for use in cryptography because deciphering the seed could lead to decryption of the hidden number sequence. Some functions exist to create cryptographically secure pseudo-random numbers in Javascript, but they are not supported by older browsers.

In this blog post, we’ll first cover the canonical methods of creating Javascript random numbers. Then we’ll move onto ways of obtaining higher-quality random data; your needs will determine the worthwhile effort.

API

• : Utilizes
• : Utilizes
• : Utilizes
• : Produces a new Mersenne Twister. Must be seeded before use.

Or you can make your own!

interfaceEngine{next()number;}

Any object that fulfills that interface is an .

• : Seed the twister with an initial 32-bit integer.
• : Seed the twister with an array of 32-bit integers.
• : Seed the twister with automatic information. This uses the current Date and other entropy sources.
• : Produce a 32-bit signed integer.
• : Discard random values. More efficient than running repeatedly.
• : Return the number of times the engine has been used plus the number of discarded values.

One can seed a Mersenne Twister with the same value () or values () and discard the number of uses () to achieve the exact same state.

If you wish to know the initial seed of , it is recommended to use the function to create the seed manually (this is what does under-the-hood).

constseed=createEntropy();constmt=MersenneTwister19937.seedWithArray(seed);useTwisterALot(mt);constclone=MersenneTwister19937.seedWithArray(seed).discard(mt.getUseCount());

Random.js also provides a set of methods for producing useful data from an engine.

• : Produce an integer within the inclusive range . can be at its minimum -9007199254740992 (-2 ** 53). can be at its maximum 9007199254740992 (2 ** 53).
• : Produce a floating point number within the range . Uses 53 bits of randomness.
• : Produce a boolean with a 50% chance of it being .
• : Produce a boolean with the specified chance causing it to be .
• : Produce a boolean with / chance of it being true.
• : Return a random value within the provided within the sliced bounds of and .
• : Same as .
• : Shuffle the provided (in-place). Similar to .
• : From the array, produce an array with elements that are randomly chosen without repeats.
• : Same as
• : Produce an array of length with as many rolls.
• : Produce a random string using numbers, uppercase and lowercase letters, , and of length .
• : Produce a random string using the provided string as the possible characters to choose from of length .
• or : Produce a random string comprised of numbers or the characters of length .
• : Produce a random string comprised of numbers or the characters of length .
• : Produce a random within the inclusive range of . and must both be s.

An example of using would be as such:

constengine=MersenneTwister19937.autoSeed();constdistribution=integer(,99);functiongenerateNaturalLessThan100(){returndistribution(engine);}

Producing a distribution should be considered a cheap operation, but producing a new Mersenne Twister can be expensive.

An example of producing a random SHA1 hash:

var engine = nativeMath;var distribution =hex(false);functiongenerateSHA1(){returndistribution(engine,40);}

Генератор псевдослучайных чисел в V8

Выглядит малопонятно, будем разбираться.

Есть одна подсказка. В старых версиях V8 был комментарий: «генератор случайных чисел использует алгоритм MWC Джорджа Марсальи (George Marsaglia)». В поисковике нашлось следующее:

Так что если вам нужен PRNG, то MWC кажется неплохим выбором.

Но реализованный в V8 алгоритм непохож на типичный MWC. Вероятно, причина в том, что это не MWC, а сразу два MWC-генератора — один в строке 5, второй в строке 6, — совместно генерирующих одно случайное число в строке 9. Не стану выкладывать тут все расчёты, но каждый из этих подгенераторов имеет длину цикла примерно 230, что даёт суммарную длину генерируемой последовательности примерно 260.

Но у нас, как вы помните, 2132 возможных идентификаторов. Допустим, что соблюдается условие равномерного распределения. Тогда вероятность коллизии после случайно сгенерированных 100 млн идентификаторов должна быть менее 0,4%. Но коллизии стали возникать гораздо раньше. Наверное, мы где-то ошиблись с нашим анализом. Возможно, проблема заключается в равномерном распределении — вероятно, есть какая-то дополнительная структура в генерируемой последовательности.

Math.Random() Example

Here’s an example of the method in action:

import java.lang.Math;

class Main {
	public static void main(String[] args) {
		double number = Math.random();
		System.out.println("Random number: " + number);
	}
}

Our code returns:

As you can see, our program has returned a random number between 0 and 1. However, this number is not very useful in its current form. If we want to generate a random number for a guessing game, for instance, we would not want to have a decimal number.

In order to produce a whole number with our pseudorandom number generator, we can multiply our random number by another number and round it to the nearest whole number. For instance, suppose we wanted to generate a random number between 1 and 10. We could do so using this code:

class Main {
	public static void main(String[] args) {
		int number = (int)(Math.random() * 10);
		System.out.println("Random number: " + number);
	}
}

Here is the result of our program after running it three times:

4

6

2

As you can see, our program returns a random integer, or whole number.

Let’s break down our code. First, we declared a class called Main which stores the code for our program.

Then we used the method to generate a random number, and we multiplied that number by 10. After we multiplied the result by 10, we converted it to an integer, which rounds it to the nearest decimal place and gives us a whole number. 

Then, on the final line, we print out the message “Random number: “ to the console, followed by the random number our program generated.

If we wanted to generate a larger number, we could replace the * 10 parts of our code with another number. For instance, say we wanted to generate a number between 1 and 1000. We could do so by replacing * 10 with * 1000 like this:

class Main {
	public static void main(String[] args) {
		int number = (int)(Math.random() * 1000);
		System.out.println("Random number: " + number);
	}
}

After executing our program three times, the following response was returned:

181

914

939

JavaScript

JS Array
concat()
constructor
copyWithin()
entries()
every()
fill()
filter()
find()
findIndex()
forEach()
from()
includes()
indexOf()
isArray()
join()
keys()
length
lastIndexOf()
map()
pop()
prototype
push()
reduce()
reduceRight()
reverse()
shift()
slice()
some()
sort()
splice()
toString()
unshift()
valueOf()

JS Boolean
constructor
prototype
toString()
valueOf()

JS Classes
constructor()
extends
static
super

JS Date
constructor
getDate()
getDay()
getFullYear()
getHours()
getMilliseconds()
getMinutes()
getMonth()
getSeconds()
getTime()
getTimezoneOffset()
getUTCDate()
getUTCDay()
getUTCFullYear()
getUTCHours()
getUTCMilliseconds()
getUTCMinutes()
getUTCMonth()
getUTCSeconds()
now()
parse()
prototype
setDate()
setFullYear()
setHours()
setMilliseconds()
setMinutes()
setMonth()
setSeconds()
setTime()
setUTCDate()
setUTCFullYear()
setUTCHours()
setUTCMilliseconds()
setUTCMinutes()
setUTCMonth()
setUTCSeconds()
toDateString()
toISOString()
toJSON()
toLocaleDateString()
toLocaleTimeString()
toLocaleString()
toString()
toTimeString()
toUTCString()
UTC()
valueOf()

JS Error
name
message

JS Global
decodeURI()
decodeURIComponent()
encodeURI()
encodeURIComponent()
escape()
eval()
Infinity
isFinite()
isNaN()
NaN
Number()
parseFloat()
parseInt()
String()
undefined
unescape()

JS JSON
parse()
stringify()

JS Math
abs()
acos()
acosh()
asin()
asinh()
atan()
atan2()
atanh()
cbrt()
ceil()
clz32()
cos()
cosh()
E
exp()
expm1()
floor()
fround()
LN2
LN10
log()
log10()
log1p()
log2()
LOG2E
LOG10E
max()
min()
PI
pow()
random()
round()
sign()
sin()
sqrt()
SQRT1_2
SQRT2
tan()
tanh()
trunc()

JS Number
constructor
isFinite()
isInteger()
isNaN()
isSafeInteger()
MAX_VALUE
MIN_VALUE
NEGATIVE_INFINITY
NaN
POSITIVE_INFINITY
prototype
toExponential()
toFixed()
toLocaleString()
toPrecision()
toString()
valueOf()

JS OperatorsJS RegExp
constructor
compile()
exec()
g
global
i
ignoreCase
lastIndex
m
multiline
n+
n*
n?
n{X}
n{X,Y}
n{X,}
n$
^n
?=n
?!n
source
test()
toString()

(x|y)
.
\w
\W
\d
\D
\s
\S
\b
\B
\0
\n
\f
\r
\t
\v
\xxx
\xdd
\uxxxx

JS Statements
break
class
continue
debugger
do…while
for
for…in
for…of
function
if…else
return
switch
throw
try…catch
var
while

JS String
charAt()
charCodeAt()
concat()
constructor
endsWith()
fromCharCode()
includes()
indexOf()
lastIndexOf()
length
localeCompare()
match()
prototype
repeat()
replace()
search()
slice()
split()
startsWith()
substr()
substring()
toLocaleLowerCase()
toLocaleUpperCase()
toLowerCase()
toString()
toUpperCase()
trim()
valueOf()

Альтернатива в виде CSPRNG

Итак, нам надо было чем-то быстро заменить Math.random(). Для JavaScript существует множество других PRNG, но у нас было два условия:

• У генератора должен быть достаточно долгий период, чтобы нагенерировать 2132 идентификаторов.
• Он должен быть тщательно протестирован и иметь хорошую поддержку.

У этого решения есть три недостатка:

• В CSPRNG почти всегда используются нелинейные трансформации, и поэтому они работают медленнее, чем некриптографические альтернативы.
• Многие CSPRNG-системы нельзя рандомизировать (seed), что делает невозможным создание воспроизводимой последовательности (например, для целей тестирования).
• CSPRNG могут непредсказуемо выделяться на фоне всех остальных мер качества, отдельные из которых могут оказаться важнее для вашего проекта.

Однако есть и преимущества:

• В большинстве случаев производительности CSPRNG вполне достаточно (на моей машине я могу с помощью crypto.getRandomValues() получить в Chrome около 100 Мб/с случайных данных).
• В определённых пределах непредсказуемость подразумевает невозможность отличить результат работы генератора от истинно случайных данных. Значит, мы можем получить всё, что нам нужно, от псевдослучайной последовательности.
• Если генератор позиционируется как «криптографически безопасный», то можно предположить, что его код анализировался более тщательно и подвергался многим практическим тестам на случайность.

Я не знаю, какова длина цикла в crypto.randomBytes(). Насколько мне известно, у этой проблемы не существует решения в замкнутой форме. Могу сказать лишь, что при большом пространстве состояния и длительном потоке входящей энтропии алгоритм должен быть достаточно безопасен. Раз уж вы доверяете OpenSSL генерирование пар публичных/личных ключей, то какой смысл беспокоиться по этому поводу? После того как мы заменили Math.random() на crypto.randomBytes(), проблема коллизий исчезла.

Java Random Class

• class is part of java.util package.
• An instance of java Random class is used to generate random numbers.
• This class provides several methods to generate random numbers of type integer, double, long, float etc.
• Random number generation algorithm works on the seed value. If not provided, seed value is created from system nano time.
• If two Random instances have same seed value, then they will generate same sequence of random numbers.
• Java Random class is thread-safe, however in multithreaded environment it’s advised to use class.
• Random class instances are not suitable for security sensitive applications, better to use in those cases.

Java Random Constructors

Java Random class has two constructors which are given below:

1. : creates new random generator
2. : creates new random generator using specified seed

Java Random Class Methods

Let’s have a look at some of the methods of java Random class.

1. : This method returns next pseudorandom which is a boolean value from random number generator sequence.
2. : This method returns next pseudorandom which is double value between 0.0 and 1.0.
3. : This method returns next pseudorandom which is float value between 0.0 and 1.0.
4. : This method returns next int value from random number generator sequence.
5. nextInt(int n): This method return a pseudorandom which is int value between 0 and specified value from random number generator sequence.

Java Random Example

Let’s have a look at the below java Random example program.

Output of the above program is:

Check this post for more about Java Radom Number Generation.

Generate Random Number using Seed

There are two ways we can generate random number using seed.

The seed is the initial value of the internal state of the pseudorandom number generator which is maintained by method next(int).

Output of the above program is:

What if we pass same seed to two different random number generators?

Let’s have a look at the below program and see what happen if we pass same seed to two different random number generators.

Output of the above program is:

We can see that it will generate same random number if we pass same seed to two different random number generators.

Java 8 Random Class Methods

As you can see from above image, there are many new methods added in Java 8 to Random class. These methods can produce a stream of random numbers. Below is a simple program to generate a stream of 5 integers between 1 and 100.

That’s all for a quick roundup on Java Random Class.

Reference: API Doc

Java Math.random() between 1 to N

By default Math.random() always generates numbers between 0.0 to 1.0, but if we want to get numbers within a specific range then we have to multiple the return value with the magnitude of the range.

Example:- If we want to generate number between 1 to 100 using the Math.random() then we must multiply the returned value by 100.

Java program to generate floating-point numbers between 1 to 100.

Output:-

10.48550810115520481.26887023085449

The above program generates floating-point numbers but if we want to generate integer numbers then we must type cast the result value.

Java program to generate integer numbers between 1 to 100.

Output:-

2070

Java Random Number Generator

Let’s look at some examples to generate a random number in Java. Later on, we will also look at ThreadLocalRandom and SecureRandom example program.

1. Generate Random integer

Yes, it’s that simple to generate a random integer in java. When we create the Random instance, it generates a long seed value that is used in all the method calls. We can set this seed value in the program, however, it’s not required in most of the cases.

2. Java Random number between 1 and 10

Sometimes we have to generate a random number between a range. For example, in a dice game possible values can be between 1 to 6 only. Below is the code showing how to generate a random number between 1 and 10 inclusive.

The argument in the is excluded, so we have to provide argument as 11. Also, 0 is included in the generated random number, so we have to keep calling nextInt method until we get a value between 1 and 10. You can extend the above code to generate the random number within any given range.

7. Generate Random byte array

We can generate random bytes and place them into a user-supplied byte array using Random class. The number of random bytes produced is equal to the length of the byte array.

8. ThreadLocalRandom in multithreaded environment

Here is a simple example showing ThreadLocalRandom usage in a multithreaded environment.

Below is a sample output of my execution of the above program.

We can’t set seed value for ThreadLocalRandom instance, it will throw .

ThreadLocalRandom class also has some extra utility methods to generate a random number within a range. For example, to generate a random number between 1 and 10, we can do it like below.

ThreadLocalRandom has similar methods for generating random long and double values.

9. SecureRandom Example

You can use SecureRandom class to generate more secure random numbers using any of the listed providers. A quick SecureRandom example code is given below.

That’s all about generating a random number in Java program.

You can download the example code from our GitHub Repository.

Using ThreadLocalRandom class

You can use ThreadLocalRandom class to generate random numbers.This class got introduced in Java 7.Although java.util.Random is thread safe but multiple threads tries to access same object, there will be lot of contention and performance issue.In case of ThreadLocalRandom, each thread will generate their own random numbers and there won’t be any contention.
Let’s understand with the help of example:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

packageorg.arpit.java2blog; import java.util.concurrent.ThreadLocalRandom; publicclassThreadLocalRandomMain{ publicstaticvoidmain(Stringargs){ System.out.println(«============================»); System.out.println(«Generating 5 random integers»); System.out.println(«============================»); for(inti=;i<5;i++){ System.out.println(ThreadLocalRandom.current().nextInt()); } System.out.println(«============================»); System.out.println(«Generating 5 random doubles»); System.out.println(«============================»); for(inti=;i<5;i++){ System.out.println(ThreadLocalRandom.current().nextDouble()); } System.out.println(«============================»); System.out.println(«Generating 5 random floats»); System.out.println(«============================»); for(inti=;i<5;i++){ System.out.println(ThreadLocalRandom.current().nextFloat()); } System.out.println(«============================»); System.out.println(«Generating 5 random booleans»); System.out.println(«============================»); for(inti=;i<5;i++){ System.out.println(ThreadLocalRandom.current().nextBoolean()); } } }

Output:

============================
Generating 5 random integers
============================
-315342453
-1922639586
-19084346
-615337866
-1075097641
============================
Generating 5 random doubles
============================
0.9074981945011997
0.7626761438609163
0.4439078754038527
0.8663565773294881
0.8133933685024771
============================
Generating 5 random floats
============================
0.50696343
0.4109127
0.4284398
0.37340754
0.28446126
============================
Generating 5 random booleans
============================
false
true
false
false
true

Git Essentials

Ознакомьтесь с этим практическим руководством по изучению Git, содержащим лучшие практики и принятые в отрасли стандарты. Прекратите гуглить команды Git и на самом деле изучите это!

95

И если вы хотите генерировать последовательности, можно создать вспомогательный метод:

public static List intsInRange(int size, int lowerBound, int upperBound) {
    SecureRandom random = new SecureRandom();
    List result = new ArrayList<>();
    for (int i = 0; i < size; i++) {
        result.add(random.nextInt(upperBound - lowerBound) + lowerBound);
    }
    return result;
}

Которые вы можете использовать в качестве:

List integerList =  intsInRange3(5, 0, 10);
System.out.println(integerList);

И что приводит к:

Математика.случайная()

Класс предоставляет нам отличные вспомогательные методы, связанные с математикой. Одним из них является метод , который возвращает случайное значение в диапазоне . Как правило, он используется для генерации случайных значений процентиля.

Тем не менее, аналогично взлом – вы можете использовать эту функцию для генерации любого целого числа в определенном диапазоне:

int min = 10;
int max = 100;

int randomNumber = (int)(Math.random() * (max + 1 - min) + min);
System.out.println(randomNumber);

Хотя этот подход еще менее интуитивен, чем предыдущий. Выполнение этого кода приводит к чему-то вроде:

43

Если вы хотите работать с последовательностью, мы создадим вспомогательный метод для добавления каждого сгенерированного значения в список:

public static List intsInRange(int size, int lowerBound, int upperBound) {
    List result = new ArrayList<>();
    for (int i = 0; i < size; i++) {
        result.add((int)(Math.random() * (upperBound + 1 - lowerBound) + lowerBound));
    }
    return result;
}

И тогда мы можем назвать это так:

List integerList =  intsInRange(5, 0, 10);
System.out.println(integerList);

Который производит:

ThreadLocalRandom.nextInt()

Если вы работаете в многопоточной среде, класс предназначен для использования в качестве потокобезопасного эквивалента . К счастью, он предлагает метод nextInt () как верхней, так и нижней границей:

int randomInt = ThreadLocalRandom.current().nextInt(0, 10);
System.out.println(randomInt);

Как обычно, нижняя граница включена, в то время как верхняя граница отсутствует:

3

Аналогично, вы можете создать вспомогательную функцию для создания последовательности этих:

public static List intsInRange(int size, int lowerBound, int upperBound) {
    List result = new ArrayList<>();
    for (int i = 0; i < size; i++) {
        result.add(ThreadLocalRandom.current().nextInt(lowerBound, upperBound));
    }
    return result;
}

Которые вы можете использовать в качестве:

List integerList = intsInRange4(5, 0, 10);
System.out.println(integerList);

SplittableRandom.ints()

Менее известным классом в Java API является класс , который используется в качестве генератора псевдослучайных значений. Как следует из названия, он разбивается и работает параллельно, и на самом деле используется только тогда, когда у вас есть задачи, которые можно снова разделить на более мелкие подзадачи.

Стоит отметить, что этот класс также основан на небезопасной генерации семян-если вы ищете безопасную генерацию семян, используйте .

Класс предлагает метод , который, с нашей точки зрения, работает так же, как :

List intList = new SplittableRandom().ints(5, 1, 11)
        .boxed()
        .collect(Collectors.toList());

System.out.println(intList);

Что приводит к:

И, если вы хотите сгенерировать только одно случайное число, вы можете отказаться от коллектора и использовать с :

int randomInt = new SplittableRandom().ints(1, 1, 11).findFirst().getAsInt();
System.out.println(randomInt);

Что приводит к:

4

Вывод

В этом уроке мы подробно рассмотрели как генерировать случайные целые числа в диапазоне в Java .

Мы рассмотрели новейший и наиболее полезный метод, а также некоторые другие популярные методы выполнения этой задачи. Большинство подходов основаны на или эквивалентных классах, используемых для более конкретных контекстов.

История двух генераторов

Давайте ещё раз посмотрим на код генерирования идентификаторов:

Замечаете, в чём проблема? Два генератора довольно странно миксуются в алгоритме V8. Числа из двух потоков не объединяются по модулю 2 (xor). Вместо этого просто конкатенируются нижние 16 бит выходных данных каждого подгенератора. Похоже, проблема именно в этом. Когда мы умножим Math.random() на 64 и приведём к наименьшему (floor), то у нас останутся верхние 6 битов. Эти биты генерируются исключительно одним из двух MWC-подгенераторов.

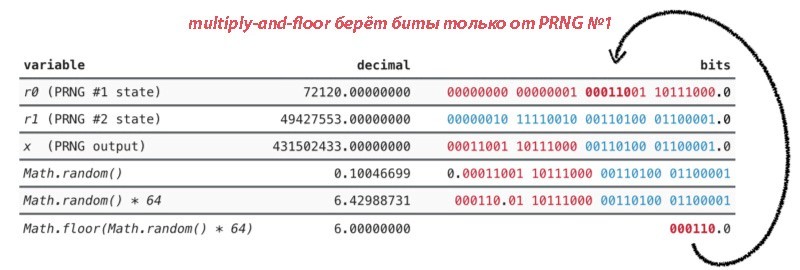
Красным выделены биты от PRNG № 1, синим — от PRNG № 2.

Но будь это так, мы почти сразу же начали бы замечать коллизии. Но мы их не замечали. Чтобы понять, почему этого не происходило, давайте вспомним пример с генерированием комбинаций из трёх чисел средствами 4-битного LCG.

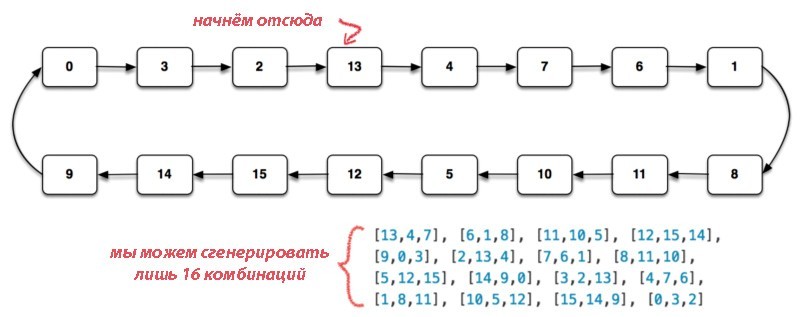
В данном случае парадокс дней рождений неприменим — последовательность даже близко нельзя назвать случайной, так что мы не можем притвориться. Очевидно, что до 17-й комбинации дублей не будет. То же самое происходит и с PRNG в V8: при определённых условиях недостаток случайности снижает вероятность того, что мы увидим коллизию.

То есть детерминированность генератора сыграла нам на руку. Но так бывает не всегда. Главный вывод, который мы сделали, заключается в том, что даже в высококачественном PRNG нельзя предполагать случайность распределения, если длина цикла не будет гораздо больше, чем количество генерируемых вами значений.

В случаях, подобных нашему, когда пытаются генерировать уникальные значения с помощью нескольких независимых последовательностей от одного генератора, беспокоятся не столько о случайности, сколько о том, чтобы последовательности не совпадали. Допустим, у нас есть N последовательностей с длиной L от генератора с периодом P. Тогда вероятность совпадения будет равна

Короче, если вы используете Math.random() в V8 и вам нужна достаточно качественная последовательность случайных чисел, то не используйте более 24 тыс. чисел. А если генерируете в несколько мощных потоков и вам нужно избегать совпадений, то вообще забудьте о Math.random().

Using random.nextInt() to generate random number between 1 and 10

We can simply use Random class’s nextInt() method to achieve this.

As the documentation says, this method call returns «a pseudorandom, uniformly distributed int value between 0 (inclusive) and the specified value (exclusive)», so this means if you call nextInt(10), it will generate random numbers from 0 to 9 and that’s the reason you need to add 1 to it.
Here is generic formula to generate random number in the range.

randomGenerator.nextInt((maximum – minimum) + 1) + minimum
In our case,
minimum = 1
maximum = 10so it will berandomGenerator.nextInt((10 – 1) + 1) + 1randomGenerator.nextInt(10) + 1

So here is the program to generate random number between 1 and 10 in java.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

packageorg.arpit.java2blog; import java.util.Random; publicclassGenerateRandomInRangeMain{ publicstaticvoidmain(Stringargs){ System.out.println(«============================»); System.out.println(«Generating 10 random integer in range of 1 to 10 using Random»); System.out.println(«============================»); Random randomGenerator=newRandom(); for(inti=;i<10;i++){ System.out.println(randomGenerator.nextInt(10)+1); } } }

When you run above program, you will get below output:

==============================
Generating 10 random integer in range of 1 to 10 using Random
==============================
1
9
5
10
2
3
2
5
8
1

Read also:Java random number between 0 and 1Random number generator in java

Random Number Generator in Java

There are many ways to generate a random number in java.

1. java.util.Random class can be used to create random numbers. It provides several methods to generate random integer, long, double etc.
2. We can also use Math.random() to generate a double. This method internally uses Java Random class.
3. class should be used to generate random number in multithreaded environment. This class is part of Java Concurrent package and introduced in Java 1.7. This class has methods similar to Java Random class.
4. can be used to generate random number with strong security. This class provides a cryptographically strong random number generator. However, it’s slow in processing. So depending on your application requirements, you should decide whether to use it or not.