Числа: целые, вещественные, комплексные

Деление с остатком Python

Оператор % используется для деления по модулю, и возвращает остаток от деления, а не частное. Это полезно, например, для нахождения множителей числа.

Деление по модулю Python (с остатком) — пример:

o = 85
p = 15
print(o % p)

Вывод

10

В этом примере 85 делится на 15. Результат – 5 с остатком 10. Значение  выводится, поскольку оператор возвращает остаток от деления.

Если мы используем два числа с плавающей точкой для деления по модулю, число с плавающей точкой будет возвращено в качестве остатка:

q = 36.0
r = 6.0
print(o % p)

Вывод

0.0

В приведенном выше примере 36.0 делится на 6.0 без остатка, поэтому возвращается значение 0.0.

Менеджеры контекста

PEP 343

• Определяет, что должен сделать менеджер контекста в начале блока, созданного оператором . Заметьте, что возвращаемое значение и есть то значение, с которым производится работа внутри .

• Определяет действия менеджера контекста после того, как блок будет выполнен (или прерван во время работы). Может использоваться для контроллирования исключений, чистки, любых действий которые должны быть выполнены незамедлительно после блока внутри with. Если блок выполнен успешно, , , и будут установлены в . В другом случае вы сами выбираете, перехватывать ли исключение или предоставить это пользователю; если вы решили перехватить исключение, убедитесь, что возвращает после того как всё сказано и сделано. Если вы не хотите, чтобы исключение было перехвачено менеджером контекста, просто позвольте ему случиться.

contextlib

Конструирование и инициализация.

Это первый метод, который будет вызван при инициализации объекта. Он принимает в качестве параметров класс и потом любые другие аргументы, которые будут переданы в . используется весьма редко, но иногда бывает полезен, в частности, когда класс наследуется от неизменяемого (immutable) типа, такого как кортеж (tuple) или строка. Я не намерен очень детально останавливаться на , так как он не то чтобы очень часто нужен, но этот метод очень хорошо и детально описан в .

Инициализатор класса. Ему передаётся всё, с чем был вызван первоначальный конструктор (так, например, если мы вызываем , получит и в качестве аргументов. почти повсеместно используется при определении классов.

Если и образуют конструктор объекта, это его деструктор. Он не определяет поведение для выражения (поэтому этот код не эквивалентен ). Скорее, он определяет поведение объекта в то время, когда объект попадает в сборщик мусора. Это может быть довольно удобно для объектов, которые могут требовать дополнительных чисток во время удаления, таких как сокеты или файловыве объекты. Однако, нужно быть осторожным, так как нет гарантии, что будет вызван, если объект продолжает жить, когда интерпретатор завершает работу. Поэтому не может служить заменой для хороших программистских практик (всегда завершать соединение, если закончил с ним работать и тому подобное)

Фактически, из-за отсутствия гарантии вызова, не должен использоваться почти никогда; используйте его с осторожностью!Замечание от переводчика: svetlov , что здесь автор ошибается, на самом деле всегда вызывается по завершении работы интерпретатора.

Создание произвольных последовательностей

Магия контейнеров

• Как найти процент от числа? формула с примерами

  Возвращает количество элементов в контейнере. Часть протоколов для изменяемого и неизменяемого контейнеров.

• Определяет поведение при доступе к элементу, используя синтаксис . Тоже относится и к протоколу изменяемых и к протоколу неизменяемых контейнеров. Должен выбрасывать соответствующие исключения: если неправильный тип ключа и если ключу не соответствует никакого значения.

• Определяет поведение при присваивании значения элементу, используя синтаксис . Часть протокола изменяемого контейнера. Опять же, вы должны выбрасывать и в соответсвующих случаях.

• Определяет поведение при удалении элемента (то есть ). Это часть только протокола для изменяемого контейнера. Вы должны выбрасывать соответствующее исключение, если ключ некорректен.

• Должен вернуть итератор для контейнера. Итераторы возвращаются в множестве ситуаций, главным образом для встроенной функции и в случае перебора элементов контейнера выражением . Итераторы сами по себе объекты и они тоже должны определять метод , который возвращает .

• Вызывается чтобы определить поведения для встроенной функции . Должен вернуть обратную версию последовательности. Реализуйте метод только если класс упорядоченный, как список или кортеж.

• предназначен для проверки принадлежности элемента с помощью и . Вы спросите, почему же это не часть протокола последовательности? Потому что когда не определён, Питон просто перебирает всю последовательность элемент за элементом и возвращает если находит нужный.
• используется при наследовании от . Определяет поведение для для каждого случая, когда пытаются получить элемент по несуществующему ключу (так, например, если у меня есть словарь и я пишу когда не является ключом в словаре, вызывается ).

Возведение в степень (**)

Нетипичный оператор для большинства других языков программирования. Тем он и удобен. Парная «звёздочка» (**) выполняет классическое математическое возведение числа «a» в степень «b»:

И показатель степени, и основание могут быть отрицательными:

И дробными:

Операндов у возведения в степень также может быть несколько. В таком случае, оператор «**» работает, как право-ассоциативный (т.е. операции выполняются справа-налево):

В завершении — про приоритет операций. Если в выражении используются разные операторы, то порядок их выполнения будет следующим:

1. возведение в степень;
2. умножение, деление, целочисленное деление и деление по модулю;
3. сложение и вычитание.

Дополнительные методы и операции в Python

В эти операции входят:
• int.bit_length() — количество бит, которое необходимо, чтобы представить число в двоичном виде без учёта лидирующих нулей и знака;
• int.to_bytes(length, byteorder, *, signed=False) — метод возвращает строку байтов, которые представляют это число;
• classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращение числа из заданной строки байтов.

Пример работы последнего метода:

>>>
>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes(, byteorder='big')
16711680

Операторы принадлежности

С помощью этих операторов можно определить, входят ли значения в определенную последовательность. Она может быть любой – строкой, списком или кортежем. К этой категории относится всего два оператора – in и not in.

In. С английского переводится, как «В». Соответственно, с помощью этого оператора осуществляется проверка, является ли определенное значение частью последовательности списка, кортежа или строки. 

Хотя принцип прост, покажем пример для наглядности. 

>>> pets=

>>> ‘fox’ in pets

Попробуйте определить, какое значение будет возвращено в этой ситуации. Правильный ответ – «False». Почему? Да, fox – это действительно лиса, и она является животным. Но она не входит в список домашних питомцев, куда относятся только собаки, коты и хорьки. Поэтому возвращается значение «ложь».

Если же написать такую строку, то будет возвращено «истина».

>>> ‘cat’ in pets

Почему? Потому что кот есть в списке питомцев. 

Теперь приведем пример проверки вхождения фразы в строку.

>>> ‘me’ in ‘disappointment’

Какой вывод будет у этой фразы? Правильно, «истина», потому что слог «me» в этом слове есть.

Not in. Этот оператор выполняет противоположное действие. Оно возвращает значение «истина» исключительно в случае, если не входит в состав последовательности та конструкция, которая находится в первом операнде.

Если бы мы в примерах выше использовали этот оператор, то были бы выданы такие результаты:

1. Если бы мы проверяли вхождение лисы в перечень домашних питомцев, то было бы выдано значение True, потому что она не входит. 
2. Если бы мы проверяли вхождение кота в этот список, было бы возвращено значение false, поскольку он также не входит. 
3. Если бы мы проверяли факт вхождения слога «me» в слово «disappointment», то был бы выдан ответ false. 

То есть, эти операторы работают полностью противоположным друг другу образом. 

Как посчитать сумму введенных чисел?

В команде input() можно передавать подсказки.

w = int(input(«Введите первое число: «)) q = int(input(«Введите второе число: «)) summa=w+q print(summa)

Введите первое число: 6 Введите второе число: 7 13

Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!

Добавляйтесь ко мне в друзья : http://vk.com/myrusakov.Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.

Если Вы не хотите пропустить новые материалы на сайте,то Вы можете подписаться на обновления: Подписаться на обновления

Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.

Порекомендуйте эту статью друзьям:

Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):

Она выглядит вот так:

BB-код ссылки для форумов (например, можете поставить её в подписи):

Арифметические операторы

Самые классические арифметические операторы – это сложение, вычитание, умножение и деление. Также рассмотрим ряд других, которые также выполняют арифметические действия.

Сложение. Соответствует математическому знаку +. Выполняет стандартную арифметическую операцию сложения. Синтаксис функции такой же, как и в математике: операнд 1 + операнд 2.

Например.

>>> 4+4

Вывод: 8.

Вычитание. Выполняет стандартную арифметическую операцию вычитания. Первый операнд – это первое число, а второй – это второе число соответственно. Сам оператор выглядит точно так же, как и математический знак минуса.

>>> 3-4

-1

Умножение. Умножает первое число на такое количество раз, которое указано во втором числе. 

Также в качестве операнд, как и во всех остальных случаях, могут использоваться переменные. В этом случае осуществляется умножение переменной 1 на переменную 2. 

>>> 5*5

25

Деление. Последовательность действий такая же самая, как и с умножением: сначала идет операнд 1, потом знак деления (/), а потом – операнд 2.

>>> 3/4

0.75 

Возведение в степень. Берет число 1 и возводит в степень числа 2.

>>> 3**4

81

Деление без остатка. Все мы знаем, что после деления может оставаться остаток, если не получается разделить число на другое число непосредственно. С помощью этого оператора мы можем получить целое число, если разделить напрямую не получается. Например.

>>> 4//3

1

>>> 10//3

3

Деление по модулю. Выполняет похожую операцию на предыдущий пример, только возвращает как раз остаток. Этот оператор – знак процента, который находится между операндами. Например:

>>> 3%4

3

Функции возведения в степень и логарифма

Эта функция принимает один параметр в виде дробного числа и возвращает .

Пример:

Вывод:

Эта функция работает так же, как и , но возвращает . Здесь, значит , то есть, .

Пример:

Вывод:

Функция log() — логарифм числа

Функция находит логарифм числа по основанию (по умолчанию). — параметр опциональный. Если нужно вычислить логарифм с определенным основанием, его нужно указать.

Пример:

Вывод:

Эта функция похожа на функцию логарифма, но добавляет к . значит , то есть, .

Пример:

Вывод:

Вычисляет логарифм по основанию 10.

Пример:

Вывод:

Функция pow() — степень числа

Используется для нахождение степени числа. Синтаксис функции . Она принимает два аргумента: основание и степень.

Пример:

Вывод:

Функция sqrt() — квадратный корень числа

Эта функция используется для нахождения квадратного корня числа. Она принимает число в качестве аргумента и находит его квадратный корень.

Пример:

Вывод:

Типы чисел в Python.

В Python числа делятся на несколько категорий в соответствии со способом их использования. Основные это целые числа (int) и вещественные (float) или числа с плавающей точкой. Чтобы узнать к какому типу относится число или переменная, можно воспользоваться встроенной функцией type(). Запустите командную строку и активируйте Python. В скобках введите число или переменную, чтобы узнать ее тип.

>>> type(5)                                                                  <class ‘int’>

>>> type(12.5)<class ‘float’>

>>> x = 10
>>> type(x)<class ‘int’>

Значение 12,5 является числом с плавающей точкой, поэтому Python выводит строку float. Переменная x содержит целое число 10, поэтому Python выводит тип int (сокращение от integer). 

7.3. Статистика

Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.

Элементарные статистические функции:

Средние значения элементов массива и их отклонения:

Корреляционные коэфициенты и ковариационные матрицы величин:

Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.

Функция преобразования углов

У внимательного читателя мог на предыдущем этапе появиться вопрос: а что, если я не знаю, сколько радиан в угле? Я знаю только количество градусов. Ничего страшного, ведь библиотека math поддерживает возможность конвертации радиан в градусы и наоборот. 

Чтобы выполнить первую задачу, существует функция degrees(), которая принимает радиан в качестве аргумента и выводит количество градусов. 

Для того, чтобы получить количество радиан, зная количество градусов, следует воспользоваться функцией radians(), которая принимает величину угла в качестве аргумента.

Запомнить очень просто. То, что мы хотим получить, так и называется функция.

Арифметические операторы Python

Как можно догадаться из названия, арифметические операторы нужны для того, чтобы совершать несложные арифметические операции. К таковым относятся:

Сложение. Для этого используется оператор +, который является таким же, как и известный математический знак, выполняющий эту функцию.
Вычитание. Эта операция осуществляется с использованием знака «–».
Умножение. В большинстве компьютерных программ данная арифметическая операция выполняется с использованием знака звездочки *. Python – не исключение.
Деление. Для этого используется знак слэша /

Внимание! Он должен быть направлен именно в эту сторону.
Остаток от деления. Выглядит так, как математический знак процента (%), но имеет другую функцию.
Возведение в степень

Отличается от аналогичного знака в арифметике. Выглядит, как две звездочки, расположенные по горизонтали (**).
Деление без остатка. Этот оператор получает исключительно целое число, округленное в меньшую сторону (так, чтобы оставался остаток). При этом он не возвращает остатка.

Теперь перейдем к описанию принципа работы этих операторов (равно, как и других). Сначала необходимо разобраться в значении слова «операнд». Это те фрагменты информации, над которыми осуществляется операция. В нашем случае – арифметическая.

Любые операнды размещаются по разные стороны оператора. В случае с математическими операторами, в большинстве случаев это будет стандартное арифметическое выражение типа a + b = c или n = a+3.

Но оператор деления по модулю, например, будет использоваться таким образом.

с = 10 % 3.

То есть, каждый из описанных выше знаков ставится между операндами. А получившееся выражение может присваиваться другой переменной или же использоваться в качестве аргумента функции.

Обратные операции

Извлечение корня

У возведения в степень две обратные операции. Первая – извлечение корня. Подробнее о корнях в Python вы можете почитать в нашей статье. Отметим лишь, что корень в питоне вычисляется с помощью той же функции pow():

Либо с применением оператора «**»:

Для извлечения квадратного корня справедливы оба вышеуказанных способа, но существует и третий, специализированный. Для его применения требуется импортировать модуль

Логарифмирование

Логарифмирование – вторая обратная операция.

Здесь – логарифм. Пример из математики – найдем значение выражения:

Легче всего эта запись читается в формате вопроса: «В какую степень нужно возвести 2, чтобы получить 16?». Очевидно, в 4-ю. Следовательно,

В питоне операция нахождения логарифма так же заложена в функционал модуля math:

Модули

Система модулей позволяет вам логически организовать ваш код на Python. Группирование кода в модули значительно облегчает процесс написания и понимания программы.
Говоря простым языком, модуль в Python это просто файл, содержащий код на Python. Каждый модуль в Python может содержать переменные, объявления классов и функций.
Кроме того, в модуле может находиться исполняемый код.

Вы можете использовать любой питоновский файл как модуль в другом файле, выполнив в нем команду . Команда в Python обладает
следующим синтаксисом:

import math
# Используем функцию sqrt из модуля math
print (math.sqrt(9))
# Печатаем значение переменной pi, определенной в math
print (math.pi)

Важно знать, что модуль загружается лишь однажды, независимо от того, сколько раз он был импортирован. Это препятствует цикличному выполнению содержимого модуля

Команда позволяет вам импортировать не весь модуль целиком, а только определенное его содержимое. Например:

# Импортируем из модуля math функцию sqrt
from math import sqrt
# Выводим результат выполнения функции sqrt.
# Обратите внимание, что нам больше незачем указывать имя модуля
print (sqrt(144))
# Но мы уже не можем получить из модуля то, что не импортировали
print (pi) # Выдаст ошибку

Выражение не импортирует весь модуль, а только предоставляет доступ к конкретным объектам, которые мы указали.

В Python так же возможно импортировать всё (переменные, функции, классы) за раз из модуля, для этого используется конструкция . Например:

from math import *
 
# Теперь у нас есть доступ ко всем функция и переменным, определенным в модуле math
 
print (sqrt(121))
print (pi)
print (e)

Однако это конструкцию следует использовать с осторожностью, поскольку при импортировании нескольких модулей можно запутаться в своем собственном коде

1. Встроенная функция range.

Встроенная функция range() используется для построения числовых последовательностей. В примере используем команду и функцию range для выполнения ровно 10 итераций с выводом значения от 0 до 10.

>>> for x in range(10)
…     print(x, end=’ ‘)
…0 1 2 3 4 5 6 7 8 9

При передаче только одного аргумента, последовательность будет начинаться с 0 и до значения аргумента (10), не включая его. Одна из самых распрастранённых ошибок, это когда разработчик предполагает, что значение аргумента функции range включается в сгенерированную последовательность. 

Приведем пример с двумя аргументами. Выведем последовательность от 20 до 30.

>>> for x in range(20, 30)
…     print(x, end=’ ‘)
…20 21 22 23 24 25 26 27 28 29

2.2. Создание числового списка с помощью функции range. 

С помощью функции range удобно строить числовые списки. 

>>> numbers = list(range(5, 25))
>>> print(numbers)

Функция range может создавать последовательности, пропуская числа в заданном диапозоне. Например приведем пример построения списка от 0 до 100, с шагом 15.

>>> numbers = list(range(0, 100, 15))
>>> print(numbers)

С помощью цикла for и функции range можно создавать практически любой числовой список. К примеру, создадим список квадратов всех числе от 1 до 10. Операция возведения в степень обозначается двумя звездочками (**).

>>> a = []
>>> for i in range(1, 11)
…     a.append(i**2)
…
>>> print(a)

На каждом цикле переменная возводится в квадрат и добавляется в список. 

Создание словаря

Пустой словарь можно создать при помощи функции или
пустой пары фигурных скобок (вот почему фигурные скобки
нельзя использовать для создания пустого множества). Для создания словаря
с некоторым набором начальных значений можно использовать следующие конструкции:

Capitals = {'Russia': 'Moscow', 'Ukraine': 'Kiev', 'USA': 'Washington'}
Capitals = dict(Russia = 'Moscow', Ukraine = 'Kiev', USA = 'Washington')
Capitals = dict()
Capitals = dict(zip(, ))
print(Capitals)

Первые два способа можно использовать только для создания небольших словарей, перечисляя все их элементы.
Кроме того, во втором способе ключи передаются как именованные параметры функции , поэтому
в этом случае ключи могут быть только строками, причем являющимися корректными идентификаторами.
В третьем и четвертом случае можно создавать большие словари, если в качестве аргументов
передавать уже готовые списки, которые могут быть получены не обязательно перечислением всех элементов,
а любым другим способом построены по ходу исполнения программы. В третьем способе
функции нужно передать список, каждый элемент которого является кортежем
из двух элементов: ключа и значения. В четвертом способе используется функция ,
которой передаются два списка одинаковой длины: список ключей и список значений.

7.5. Дискретное преобразование Фурье

Если данные в ваших массивах — это сигналы: звуки, изображения, радиоволны, котировки акций и т.д., то вам наверняка понадобится дискретное преобразование Фурье. В NumPy представлены методы быстрого дискретного преобразования Фурье для одномерных, двумерных и многомерных сигналов, а так же некоторые вспомогательные функции. Рассмотрим некоторые простые примеры.

Одномерное дискретное преобразование Фурье:

Двумерное дискретное преобразование Фурье:

Очень часто при спектральном анализе используются оконные функции (оконное преобразование Фурье), некоторые из которых так же представлены в NumPy

Функция экспоненты exp() в Python

Библиотека Math в Python поставляется с функцией , которую можно использовать для вычисления значения . К примеру, — экспонента от . Значение равно .

Метод может быть использован со следующим синтаксисом:

Python

math.exp(x)

1	math.exp(x)

Параметр может быть положительным или отрицательным числом. Если не число, метод возвращает ошибку. Рассмотрим пример использования данного метода:

Python

import math

# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00

# Передача значений методу exp() и вывод
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))

1 2 3 4 5 6 7 8 9 10 11

importmath   # Инициализация значений an_int=6 a_neg_int=-8 a_float=2.00   # Передача значений методу exp() и вывод print(math.exp(an_int)) print(math.exp(a_neg_int)) print(math.exp(a_float))

Вывод

Shell

403.4287934927351
0.00033546262790251185
7.38905609893065

1 2 3

403.4287934927351 0.00033546262790251185 7.38905609893065

Мы объявили три переменные и присвоили им значения с различными числовыми типами данных. Мы передали значения методу для вычисления их экспоненты.

Мы также можем применить данный метод для встроенных констант, что продемонстрировано ниже:

Python

import math

print(math.exp(math.e))
print(math.exp(math.pi))

1 2 3 4

importmath print(math.exp(math.e)) print(math.exp(math.pi))

Вывод

Shell

15.154262241479262
23.140692632779267

1 2	15.154262241479262 23.140692632779267

При передаче не числового значения методу будет сгенерирована , как показано далее:

Python

import math

print(math.exp(«20»))

1 2 3

importmath print(math.exp(«20»))

Вывод

Shell

Traceback (most recent call last):
File «C:/Users/admin/mathe.py», line 3, in <module>
print (math.exp(«20»))
TypeError: a float is required

1 2 3 4

Traceback(most recent call last) File»C:/Users/admin/mathe.py»,line3,in<module> print(math.exp(«20»)) TypeErrorafloatisrequired

Как видно из примера выше, генерируется ошибка .

Квадратный корень

Положительное число

Именно на работу с неотрицательными числами «заточена» функция

Если число больше или равно нулю, то неважно, какой у него тип. Вы можете извлекать корень из целых чисел:

А можете – из вещественных:

Легко проверить корректность полученных результатов с помощью обратной операции возведения в степень:

Отрицательное число

Функция не принимает отрицательных аргументов. Только положительные целые числа, вещественные числа и ноль.

Такая работа функции идёт вразрез с математическим определением. В математике корень спокойно извлекается из чисел меньше 0. Вот только результат получается комплексным, а таким он нужен для относительно узкого круга реальных задач, вроде расчетов в сфере электроэнергетики или физики волновых явлений.

Поэтому, если передадите отрицательное число в , то получите ошибку:

Целые числа (int)

В Python любое число, состоящее из десятичных цифр без префикса, интерпретируется как десятичное число типа

Целые числа в Python представлены только одним типом – PyLongObject, реализация которого лежит в longobject.c, а сама структура выглядит так:

Любое целое число состоит из массива цифр переменной длины, поэтому в Python 3 в переменную типа может быть записано число неограниченной длины. Единственное ограничение длины – это размер оперативной памяти.

Целые числа могут записываться не только как десятичные, но и как двоичные, восьмеричные или шестнадцатеричные. Для этого перед числом нужно написать символы:

• 0b (0B) – для двоичного представления;
• 0o (0O) – для восьмеричного представления;
• 0x (0X) – для шестнадцатеричного представления.

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File "", line 1, in
OverflowError: int too large to convert to float

Простенькие примеры работы с числами:

>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d - c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137

Операторы присваивания Python

Присваивание значения переменной – одна из самых распространенных операций. С ее помощью можно передавать ей необходимую информацию, которая в дальнейшем может использоваться программой. Без нее невозможно представить программирования. А для большего удобства использования количество операторов присваивания в Python очень большое. 

Рассмотрим наиболее распространенные из них.

Оператор =. Это классический оператор присваивания

Обратите внимание, он не проверяет равенство операндов, за это отвечает другой оператор. Он именно используется для присваивания значений или объектов переменным

Тем не менее, в некоторых случаях он может читаться, как знак «равно», но только если речь не идет о сравнении операндов.

Пример.

x = 5. 

Эта простая строчка кода присваивает переменной x значение 5. То есть, она может читаться, как «x равно 5». Но при этом осуществляется не констатация факта, а действие, после которого переменная x становится равной 5. А до этого действия она может как вовсе отсутствовать, так и содержать любое другое значение. 

Это единственный оператор этой категории, который выполняет одно действие. Остальные же совершают сразу 2.

Оператор +=. Этот оператор сначала добавляет к переменной то число, которое находится во втором операнде, а потом делает так, чтобы эта переменная имела соответствующее значение. 

x += 3

Это то же самое, что x = x + 3.

В целом, любой из операторов может быть заменен на аналогичное выражение, где переменная равно переменная, оператор, операнд 2. Дальше мы приведем еще несколько таких примеров для наглядности, и такая же логика будет действовать для всех операторов присваивания.

Оператор –=. Выполняет похожую операцию на ту, что делает предыдущий оператор, но при этом со знаком «минус». Он сначала берет переменную, которая стоит в первом операнде, отнимает от содержащегося в ней числе значение, расположенное в правом операнде, а потом результат присваивает этой же переменной, которая стоит в левом операнде. 

На практике все значительно проще, чем может показаться, когда вы читали это правило. Оператор –= аналогичен выражению x = x-y. Просто оно более сокращенное. 

Приведем пример.

x -= 3

Если вместо x подставить значение 2, то получится число -1, поскольку если от двух отнять 3, выйдет именно -1.

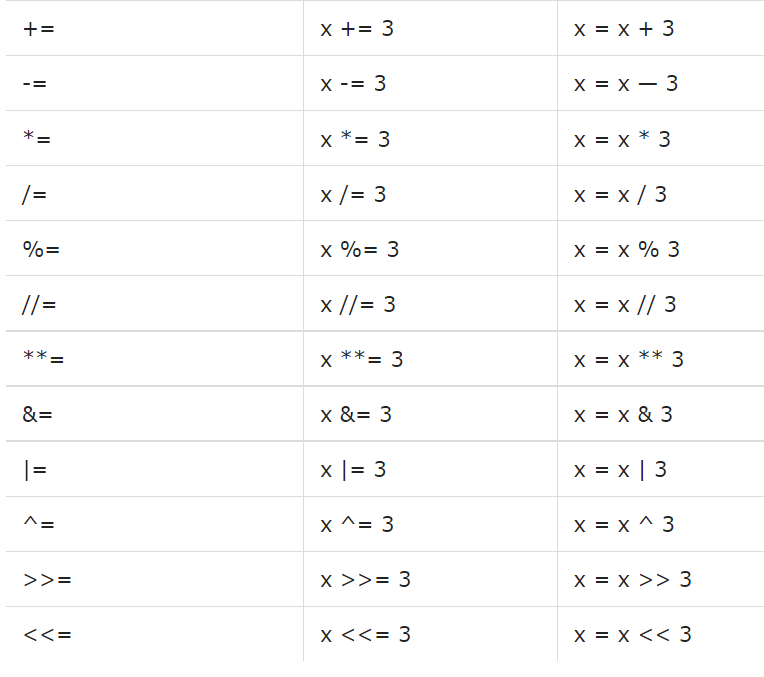
Оператор *=. Аналог предыдущих двух операторов присваивания, только выполняющий операцию умножения. Соответственно, принцип его работы аналогичный. 

В целом, по такому же принципу работают все остальные операторы. Например, есть оператор деления, который также ставится перед знаком равно, а также деление по модулю, остаток от деления и так далее. Давайте приведем таблицу с описанием всех имеющихся операторов сравнения при их соединении с другими.