Тангенс (tg x) и котангенс (ctg x)

Вычисление значения арктангенса

Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.

Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:

Способ 1: ручной ввод функции

Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.

1. Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:

Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:

Универсальная тригонометрическая подстановка

Основные тригонометрические формулы завершаются такими формулами, которые выражают функции тригонометрии через тангенс половинного угла.Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.

Универсальная тригонометрическая подстановка

Эти формулы выражаются через тангенс половинного угла.

Итак, мы написали самые простые и самые основные формулы, которые необходимо знать каждому учащемуся. Ведь именно при их помощи изучается тригонометрия. Кроме того, многие формулы необходимо знать для более эффективной подготовки к ЕГЭ.

характеристики

Происхождение касательной функции от углового перемещения в единичной окружности

периодичность

Касательная и котангенс — периодические функции с периодом , так что это верно .
π{\ displaystyle \ pi}загар⁡(Икс+π)знак равнозагар⁡(Икс){\ Displaystyle \ загар (х + \ пи) = \ загар (х)}

однообразие

Касательная: строго монотонно возрастающая в соответствующем интервале.

Котангенс: строго монотонно убывающий в соответствующем интервале.

Симметрии

Точка, симметричная началу координат:

загар⁡(-Икс)знак равно-загар⁡Иксдетская кроватка⁡(-Икс)знак равно-детская кроватка⁡Икс{\ Displaystyle \ загар (-x) = — \ загар х \ qquad \ qquad \ cot (-x) = — \ cot x}

нулевая точка

Касательная:	Иксзнак равноп⋅π;п∈Z{\ Displaystyle х = п \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}
Котангенс:	Иксзнак равно(12+п)⋅π;п∈Z{\ displaystyle x = \ left ({\ frac {1} {2}} + n \ right) \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}

Поляки

Касательная:	Иксзнак равно(12+п)⋅π;п∈Z{\ displaystyle x = \ left ({\ frac {1} {2}} + n \ right) \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}
Котангенс:	Иксзнак равноп⋅π;п∈Z{\ Displaystyle х = п \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}

Поворотные моменты

Касательная:	Иксзнак равноп⋅π;п∈Z{\ Displaystyle х = п \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}
Котангенс:	Иксзнак равно(12+п)⋅π;п∈Z{\ displaystyle x = \ left ({\ frac {1} {2}} + n \ right) \ cdot \ pi \ ,; \ quad n \ in \ mathbb {Z}}

И функция тангенса, и функция котангенса имеют асимптоты, но не имеют скачков или экстремумов.

Формулы общего вида

Определения

Синус угла α (обозн. sin(α)) — отношение противолежащего от угла α катета к гипотенузе.

Косинус угла α (обозн. cos(α)) — отношение прилежащего к углу α катета к гипотенузе.

Тангенс угла α (обозн. tg(α)) — отношение противолежащего к углу α катета к прилежащему. Эквивалентное определение — отношение синуса угла α к косинусу того же угла — sin(α)/cos(α).

Котангенс угла α (обозн. ctg(α)) — отношение прилежащего к углу α катета к противолежащему. Эквивалентное определение — отношение косинуса угла α к синусу того же угла — cos(α)/sin(α).

Другие тригонометрические функции: секанс — sec(α) = 1/cos(α); косеканс — cosec(α) = 1/sin(α).

Примечание

Мы специально не пишем знак * (умножить), — там, где две функции записаны подряд, без пробела, он подразумевается.

Подсказка

Для вывода формул косинуса, синуса, тангенса или котангенса кратных (4+) углов, достаточно расписать их по формулам соотв. косинуса, синуса, тангенса или котангенса суммы, либо сводить к предыдущим случаям, сводя до формул тройных и двойных углов.

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Обратные функции

Биекции получаются соответствующим ограничением областей определения :

касательная

загар-π2,π2→Р.{\ displaystyle \ tan \ двоеточие \; \ left] — {\ tfrac {\ pi} {2}}, \, {\ tfrac {\ pi} {2}} \ right [\ to \ mathbb {R}}.

Ваша обратная функция

арктанР.→-π2,π2{\ displaystyle \ operatorname {arctan} \ двоеточие \ mathbb {R} \ to \, \ left] — {\ tfrac {\ pi} {2}}, \, {\ tfrac {\ pi} {2}} \ right [}

называется арктангенсом и поэтому также биективен.

котангенс

детская кроватка,π→Р.{\ Displaystyle \ кроватка \ двоеточие] 0, \, \ пи [\ к \ mathbb {R}}.

Ваша обратная функция

арккотР.→,π{\ Displaystyle \ OperatorName {arccot} \ двоеточие \ mathbb {R} \ to \,] 0, \, \ pi [}

называется аркотангенсом и поэтому также биективен.

Дифференциальное уравнение

Касательная — это решение уравнения Риккати

ш′знак равно1+ш2{\ Displaystyle ш ‘= 1 + ш ^ {2}}.

Факторинг правой стороны дает

ш′знак равно1+ш2знак равно(ш+я)(ш-я){\ Displaystyle вес ‘= 1 + вес ^ {2} = (вес + \ mathrm {i}) (w- \ mathrm {i})}

с мнимой единицей . Касательный (как комплексная функция) имеют исключительные значения , : Эти значения не принимается , поскольку функции постоянных и решение дифференциального уравнения и существования и теорема единственности исключает , что два различных решения имеют то же значение , в том же месте.
я{\ Displaystyle \ mathrm {я}}я{\ Displaystyle \ mathrm {я}}-я{\ displaystyle — \ mathrm {i}}я{\ Displaystyle \ mathrm {я}}-я{\ displaystyle — \ mathrm {i}}

Сложный аргумент

загар⁡(Икс+я⋅у)знак равногрех⁡(2Икс)потому что⁡(2Икс)+шиш⁡(2у)+ягрех⁡(2у)потому что⁡(2Икс)+шиш⁡(2у){\ Displaystyle \ загар (х + \ mathrm {я} \! \ cdot \! y) = {\ frac {\ sin (2x)} {\ cos (2x) + \ cosh (2y)}} + \ mathrm { i} \; {\ frac {\ sinh (2y)} {\ cos (2x) + \ ch (2y)}}}   С участием Икс,у∈Р.{\ displaystyle x, y \ in \ mathbb {R}}

детская кроватка⁡(Икс+я⋅у)знак равно-грех⁡(2Икс)потому что⁡(2Икс)-шиш⁡(2у)+ягрех⁡(2у)потому что⁡(2Икс)-шиш⁡(2у){\ Displaystyle \ кроватка (х + \ mathrm {я} \! \ cdot \! y) = {\ frac {- \ sin (2x)} {\ cos (2x) — \ cosh (2y)}} + \ mathrm {i} \; {\ frac {\ sinh (2y)} {\ cos (2x) — \ ch (2y)}}}   С участием Икс,у∈Р.{\ displaystyle x, y \ in \ mathbb {R}}

Тригонометрия в Excel: основные функции

Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.

Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.

Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A(1, ) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

                                     

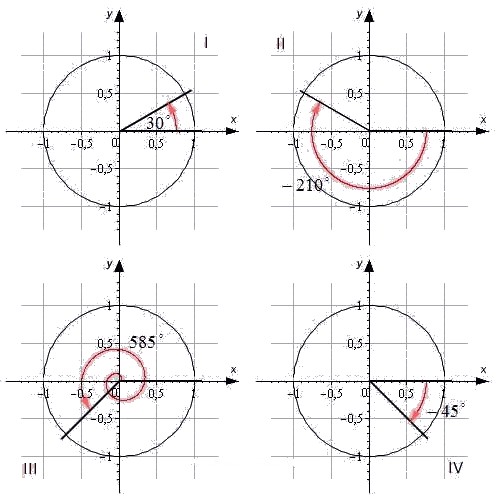
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

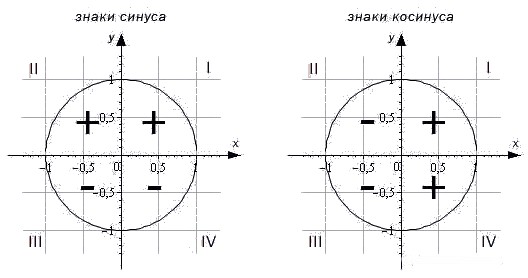
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

                                  

Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям. 

                                 

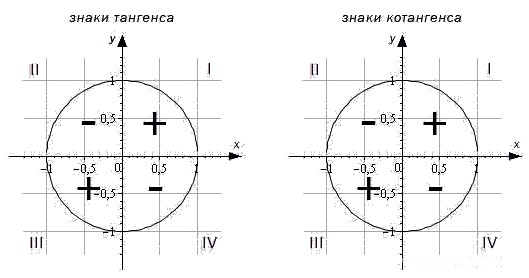
Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
3. Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
4. Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Тангенс угла

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения. Введя функции угла, определяют их свойства

Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

График синуса и косинуса

Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .

Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).

Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.

Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.

Мы знаем, что

sin 0 = 0

sin π/6 = 1/2

sin π/2 = 1

Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.

Теперь построим график косинуса. Мы знаем что

cos 0 = 1

cos π/3 = 1/2

cos π/2 = 1

Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:

sin (x+ 2π) = sinx

cos (x+ 2π) = sinx

В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие

f(x) = – f(– x)

Если f(x) – четная ф-ция, то должно выполняться условие:

f(x) = f(– x)

Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:

Поэтому верны формулы:

sin (– α) = – sinα

cos (– α) = cosα

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:

Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:

Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла

Связь определений из геометрии и тригонометрии

Если рассматривать угол поворота α величиной от до 90 градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.

Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0). Повернем ее на угол α величиной от до 90 градусов, получим точку A₁(x, y). Опустим из точки А₁ на ось Ox перпендикуляр A₁H.

Легко видеть, что в прямоугольном треугольнике угол A₁OH равен углу поворота α, длина прилежащего к этому углу катета OH равна абсциссе точки A₁, то есть, |OH|=x, длина противолежащего к углу катета A₁H равна ординате точки A₁, то есть, |A₁H|=y, а длина гипотенузы OA₁ равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α в прямоугольном треугольнике A₁OH равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A₁H|/|OA₁|=y/1=y. А по определению из тригонометрии синус угла поворота α равен ординате точки A₁, то есть, sinα=y. Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α при α от до 90 градусов.

Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α.

Список литературы.

1. Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений / . — 20-е изд. М.: Просвещение, 2010. — 384 с.: ил. — ISBN 978-5-09-023915-8.
2. Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. — 2-е изд — М.: Просвещение, 2001. — 224 с.: ил. — ISBN 5-09-010803-X.
3. Алгебра и элементарные функции: Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
4. Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
5. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
6. Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. — 4-е изд., доп. — М.: Мнемозина, 2007. — 424 с.: ил. ISBN 978-5-346-00792-0.
7. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни /; под ред. А. Б. Жижченко. — 3-е изд. — И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
8. Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
9. Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Применение: тангенс и угол наклона

Пример наклона

Касательная представляет собой важную фигуру для линейных функций : каждая линейная функция

жР.→Р.,Икс↦мИкс+c{\ Displaystyle е \ двоеточие \ mathbb {R} \ to \ mathbb {R}, \; x \ mapsto mx + c}

имеет прямую линию в виде графика . Тангенс (ориентированного) угла между положительным направлением оси x и прямой линией — это наклон прямой линии, т. Е. ЧАС

Неважно, какую из двух полуосей вы выберете в качестве ответной ноги.
α{\ displaystyle \ alpha} м{\ displaystyle m}мзнак равнозагарα{\ Displaystyle м = \ загар \, \ альфа}

Под также понимается тангенс угла уклона. Пример на рисунке справа показывает уклон 10%, соответствующий углу наклона около 5,7 ° с тангенсом 0,1.

Теоремы сложения

Теоремы сложения для касательной и котангенса следующие:

загар⁡(Икс±у)знак равнозагар⁡Икс±загар⁡у1∓загар⁡Иксзагар⁡у,детская кроватка⁡(Икс±у)знак равнодетская кроватка⁡Иксдетская кроватка⁡у∓1детская кроватка⁡у±детская кроватка⁡Икс{\ displaystyle \ tan (x \ pm y) = {\ frac {\ tan x \ pm \ tan y} {1 \ mp \ tan x \ tan y}} \ ,, \ qquad \ cot (x \ pm y) = {\ frac {\ cot x \ cot y \ mp 1} {\ cot y \ pm \ cot x}}}

Из теорем сложения, в частности, для двойных углов следует

загар⁡(2Икс)знак равно2загар⁡Икс1-загар2⁡Икс,детская кроватка⁡(2Икс)знак равнодетская кроватка2⁡Икс-12детская кроватка⁡Икс{\ displaystyle \ tan (2x) = {\ frac {2 \ tan x} {1- \ tan ^ {2} x}} \ ,, \ qquad \ cot (2x) = {\ frac {\ cot ^ {2 } x-1} {2 \ cot x}}}

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла  — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:
 

tg2α + 1 =

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

1 + ctg2α =

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
 

1. Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
2. В результате деления получаем формулу tg2α + 1 =
3. Если обе части основного тригонометрического  тождества sin2α + cos2α = 1 разделить на  sin2α, где синус не равен нулю, то получим тождество:
   1 + ctg2α = . 
4. Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
5. А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число. 

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами. 

Основные тригонометрические тождества

1	sin2α + cos2α = 1
2
3
4	tgα * ctgα = 1
5	tg2α + 1 =
6	1 + ctg2α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Таблица синусов и её применение

Для начала нужно напомнить, что означает такое понятие, как синус угла.

Синус – это отношение противолежащего этому углу катета к гипотенузе.

Это справедливо в случае, если треугольник прямоугольный.

Стандартный прямоугольный треугольник: стороны a (BC) и b (AC) – катеты, сторона с (AB) – гипотенуза

Как известно, целых значений угла – 360. Но часто нужно рассчитать значения для самых популярных углов, таких как: синус 0°, синус 30°, синус 45°, синус 60°, синус 90°. Эти значения можно найти в таблицах Брадиса.

Несмотря на то, что в 2021 году она отмечает свой столетний юбилей, свою актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов. Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.

Вычисление котангенса числа или любого угла

\(ctg\: t=\)\(\frac{cos\:⁡t}{sin\:⁡t}\)

Пример. Вычислите \(ctg\: \frac{5π}{6}\).Решение: Найдем сначала \(\frac{5π}{6}\) на круге. Затем найдем \(cos\:⁡\frac{5π}{6}\) и \(sin\:\frac{5π}{6}\), а потом поделим одно на другое.

\(ctg\:\frac{5π}{6}=\)\(\frac{cos⁡\:\frac{5π}{6}}{sin⁡\:\frac{5π}{6}}\)\(=-\frac{\sqrt{3}}{2}:\frac{1}{2}=-\frac{\sqrt{3}}{2} \cdot \frac{2}{1}=-\sqrt{3}\)

Ответ: \(-\sqrt{3}\).

Пример. Вычислите \(ctg\:\frac{π}{2}\).

Решение: Чтобы найти котангенс пи на \(2\) нужно найти сначала косинус и синус \(\frac{π}{2}\). И то, и другое найдем с помощью тригонометрического круга:

Точка \(\frac{π}{2}\) на числовой окружности совпадает с \(1\) на оси синусов, значит \(sin\:\frac{π}{2}=1\). Если из точки \(\frac{π}{2}\) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку \(0\), значит \(cos\:⁡\frac{π}{2}=0\). Получается: \(ctg\:\frac{π}{2}=\)\(\frac{cos\:⁡\frac{π}{2}}{sin\:⁡\frac{π}{2}}\)\(=\)\(\frac{0}{1}\)\(=0\).

Ответ: \(0\).

Пример. Вычислите \(ctg\:(-765^\circ)\).Решение:   \(ctg\: (-765^\circ)=\)\(\frac{cos\:(-⁡765^\circ)}{sin\:⁡(-765^\circ)}\)
Что бы вычислить синус и косинус \(-765^°\). Отложим \(-765^°\) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на \(720^°\) , а потом еще на \(45^°\).

\(sin⁡(-765^°)=-\frac{\sqrt{2}}{2}\);
\(cos⁡(-765^°)=\frac{\sqrt{2}}{2}\) ;
получается \(ctg(-765^°)= \frac{\sqrt{2}}{2} ∶ -\frac{\sqrt{2}}{2}=-1\).

Ответ: \(-1\).

Пример. Найдите \(ctg\:\frac{π}{3}\).Решение:   \(ctg\: \frac{π}{3}=\)\(\frac{cos\:⁡\frac{π}{3}}{sin\:⁡\frac{π}{3}}\). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
\(sin⁡(\frac{π}{3})=\frac{\sqrt{3}}{2}\);
\(cos⁡(\frac{π}{3})=\frac{1}{2}\) ;
получается \(ctg(\frac{π}{3})=\frac{1}{2} ∶ \frac{\sqrt{3}}{2}= \frac{1}{2} \cdot \frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}}\).

Ответ: \(\frac{1}{\sqrt{3}}\).

Однако можно определять значение котангенса и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.

Чтобы определить значение котангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу котангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси котангенсов.
3) Найти координату пересечения этой прямой и оси.

Пример. Вычислите \(ctg\:\frac{π}{4}\).Решение:   
1) Отмечаем \(\frac{π}{4}\) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется \(1\).

Ответ: \(1\).

Пример. Найдите значение \(ctg\: 30°\) и \(ctg\: (-60°)\).Решение:   
Для угла \(30°\) (\(∠COA\)) котангенс будет равен \(\sqrt{3}\) (приблизительно \(1,73\)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось котангесов.
\(ctg\;(-60°)=\frac{\sqrt{3}}`3`\) (примерно \(-0,58\)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.