Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

2.3.2. Синус и косинус window.top.document.title = «2.3.2. Синус и косинус»;

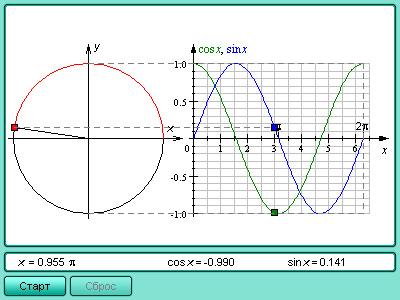
Положение точек на координатной окружности можно задавать не только длиной дуги, но и декартовыми координатами. Построим декартову систему координат с центром в точке O, осью абсцисс, проходящей через начало отсчета A (0), и осью ординат, проходящей через точку

За единицу отсчета возьмем радиус этой окружности. Декартовы координаты точки M (x) единичной окружности называются косинусом и синусом числа x:

Модель 2.9. Координатная окружность

Для

определение синуса и косинуса совпадает с геометрическим определением этих понятий, заданных при помощи прямоугольного треугольника OPM. В этом случае

Так как координаты точек окружности единичного радиуса по модулю не превосходят 1, то

Таким образом, областью значений обеих функций является отрезок .

Ниже приведены значения косинуса и синуса для некоторых значений x:

x 30° 45° 60° 90° 180° 270° sin x 1 –1 cos x 1 –1

Таблица 2.3.2.1

Функция sin x обращается в нуль при x = πn, функция cos x обращается в нуль при

График 2.3.2.1.Графики функций y = sin x и y = cos x.

in xcos x

Промежутки монотонности и знакопостоянства:

Функция sin x Неотрицателен, возрастает от 0 до 1 Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 cos x Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 Неотрицателен, возрастает от 0 до 1

Таблица 2.3.2.2

Синус достигает максимума в точках

и минимумы в точках

Косинус достигает максимума в точках x_max = 2πn, минимума – в точках x_min = π + 2πn.

Функция sin x нечетна, функция cos x четна:

Формулы приведения, позволяющие свести тригонометрические функции от любого аргумента к функциям от углов из промежутка

Основное тригонометрическое тождество (следствие теоремы Пифагора):

Некоторые тригонометрические формулы приведены в таблице.

График функции y = sin x называется синусоидой, а функции y = cos x – косинусоидой. В обоих случаях достаточно построить графики на отрезке или , а затем периодически продолжать их на всю ось. Более того, достаточно построить график y = sin x на отрезке

отразить симметрично относительно оси

а затем отразить получившийся график относительно точки (π; 0). График y = cos x после построения на отрезке

нужно отразить относительно точки

а затем получившийся график – относительно оси x = π. Заметим также, что косинусоида получается из синусоиды сдвигом на π/2 влево, поэтому, как правило, используется только термин «синусоида».

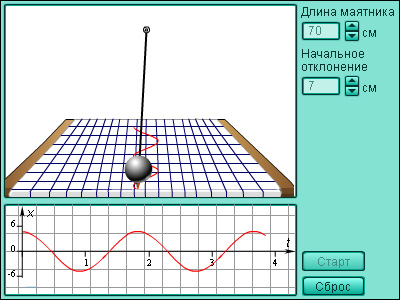
Модель 2.10. Математический маятник

Синус и косинус применяются во многих областях физики и математики. Например, с их помощью удобно описывать гармонические колебания, задаваемые формулами y = A cos (ωx + φ) или y = A sin (ωx + φ). Здесь A – амплитуда, ω – частота, φ – начальная фаза колебаний. Для построения графика гармонического колебания необходимо последовательно выполнить следующие операции над синусоидой:

• сжать к оси ординат с коэффициентом ω,
• перенести вдоль оси абсцисс на φ влево,
• растянуть от оси абсцисс в A раз.

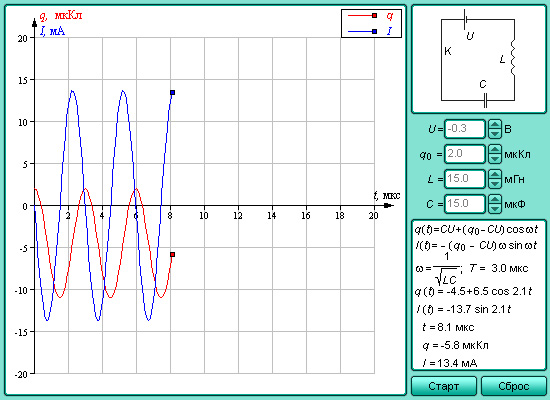
Если мы имеем дело с явлением, в котором одновременно происходят несколько различных колебательных процессов с соизмеримыми периодами, то зависимость колеблющейся величины от времени остается периодической, но график этой зависимости в общем случае уже не является синусоидой. Любую из функций, описывающих эту зависимость, можно представить в виде суммы постоянной составляющей и гармонических колебаний с частотами, кратными

Модель 2.11. Колебания в электрической цепи

Особенности построения

Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:

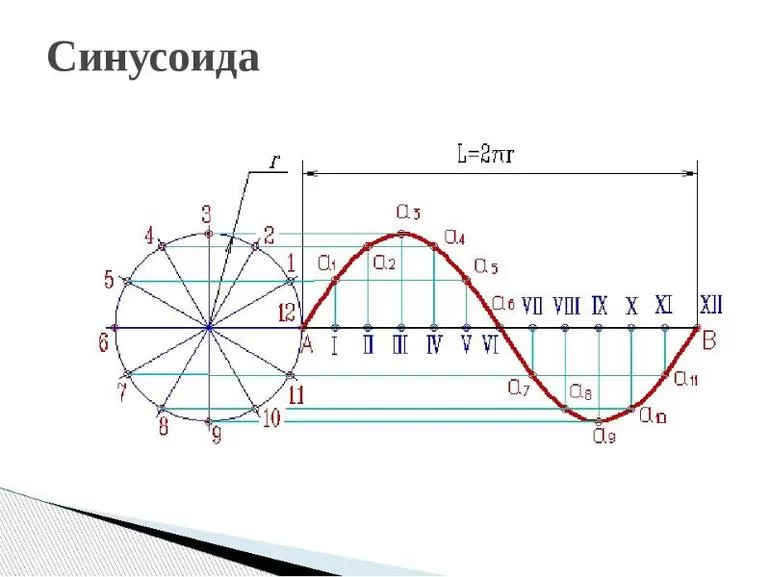
• проводится горизонтальная ось, на которой откладывается заданная длина волны;
• отрезок делится на равные части;
• слева чертится окружность с радиусом, равным величине амплитуды;
• окружность делится на 12 одинаковых частей;
• через полученные точки проводятся прямые;
• из точек проводятся перпендикуляры к оси.

График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.

Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:

• размах;
• растяжение/сжатие;
• фазовые колебания;
• круговая частота.

При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:

• А (а) — модуль неизвестной (расстояние от начала координат до точки А);
• w — угловая частота;
• t — время.

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Сведение к углу

Удобнее всего находить значения для угла от до 90 °. Сведение к углу из интервала от до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.

Пример 7

Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения.  Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.

Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от до 90° с помощью формул приведения, если угол не находится в этих пределах.

График синуса и косинуса

Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .

Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).

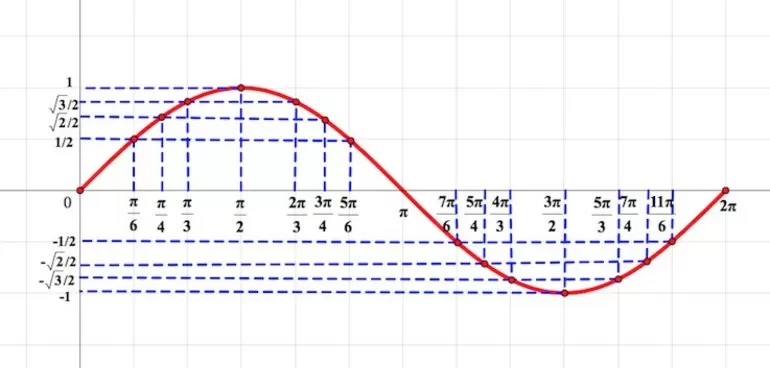
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.

Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.

Мы знаем, что

sin 0 = 0

sin π/6 = 1/2

sin π/2 = 1

Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.

Теперь построим график косинуса. Мы знаем что

cos 0 = 1

cos π/3 = 1/2

cos π/2 = 1

Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:

sin (x+ 2π) = sinx

cos (x+ 2π) = sinx

В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие

f(x) = – f(– x)

Если f(x) – четная ф-ция, то должно выполняться условие:

f(x) = f(– x)

Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:

Поэтому верны формулы:

sin (– α) = – sinα

cos (– α) = cosα

Уравнения

Общее уравнение для экспоненциально затухающей синусоиды может быть представлено как:

у ( т ) знак равно А ⋅ е — λ т ⋅ потому что ⁡ ( ω т + ϕ ) {\ Displaystyle у (т) = А \ CDOT е ^ {- \ лямбда т} \ CDOT \ соз (\ омега т + \ фи)}

куда:

у ( т ) {\ Displaystyle у (т)} — мгновенная амплитуда в момент времени t ;

А {\ displaystyle A} — начальная амплитуда огибающей;

λ {\ displaystyle \ lambda} — скорость убывания, обратная единицам времени независимой переменной t ;

ϕ {\ displaystyle \ phi} — фазовый угол при t = 0;

ω {\ displaystyle \ omega} — угловая частота ;

Другие важные параметры включают:

• Частота :, количество циклов в единицу времени. Он выражается в обратных единицах времени , или в герцах . ж знак равно ω ( 2 π ) {\ Displaystyle F = \ omega / (2 \ pi)} т — 1 {\ displaystyle t ^ {- 1}}
• Постоянная времени :, время, за которое амплитуда уменьшается в e раз . τ знак равно 1 λ {\ Displaystyle \ тау = 1 / \ лямбда}
• Период полураспада — это время, необходимое для уменьшения огибающей экспоненциальной амплитуды в 2 раза. Оно равно примерно . пер ⁡ ( 2 ) λ {\ displaystyle \ ln (2) / \ lambda} 0,693 λ {\ displaystyle 0.693 / \ lambda}
• Коэффициент демпфирования : безразмерная характеристика скорости затухания относительно частоты, приблизительно или точно . ζ {\ displaystyle \ zeta} ζ знак равно λ ω {\ displaystyle \ zeta = \ lambda / \ omega} ζ знак равно λ λ 2 + ω 2 < 1 {\ displaystyle \ zeta = \ lambda / {\ sqrt {\ lambda ^ {2} + \ omega ^ {2}}} <1}
• Q-фактор : это еще одна безразмерная характеристика величины демпфирования; высокий Q указывает на медленное затухание по отношению к колебаниям. Q знак равно 1 ( 2 ζ ) {\ Displaystyle Q = 1 / (2 \ zeta)}

Значения основных функций тригонометрии

Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.

Определение 3

Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 . 

Определение 4

Тангенс по известному косинусу tg2α+1=1cos2α . 

Определение 5

Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α . 

Определение 6

Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 . 

Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере

Пример 6

Необходимо найти значение синуса угла π8, если tg π8=2-1 . 

Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1  Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеемsin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24

Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 .  sin π8=2-22.

Основные понятия

Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:

• a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
• b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
• c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
• d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).

Общая схема построения графика функциис помощью геометрических преобразований

Рассмотрим функцию , которая «базируется» на некоторой функции . Для многих читателей алгоритм построения графика уже понятен:

– на первом шаге выполняем преобразования, связанные с АРГУМЕНТОМ функции (см. первые два параграфа), в результате чего получаем график функции ;

– на втором шаге выполняем только что рассмотренные преобразования, связанные с самой ФУНКЦИЕЙ, и получаем график .

Завершим самое длинное построение данного урока:

Пример 19 (концовка Примера 10)

Построить график функции

В примере №10 мы выполнили построение графика , то есть полностью разобрались с аргументом функции. И сейчас осталось выполнить завершающие шаги.

График функции :

4) отобразим симметрично относительно оси : ;
5) сдвинем вдоль оси  на 3 единицы вверх: :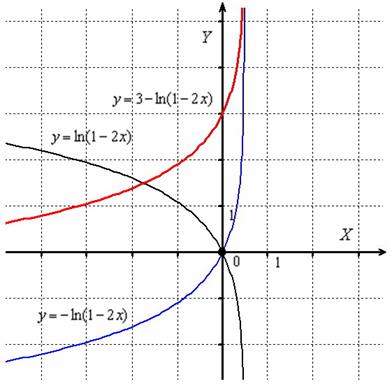

На практике, к счастью, построения почти всегда более коротки, например:

 – кубическую параболу  сдвигаем вдоль оси  на 5 единиц вправо и сжимаем вдоль оси  в 3 раза.

 – график экспоненты отображаем симметрично относительно оси ординат, затем – симметрично относительно оси абсцисс.

 – график функции  смещаем влево на 5 единиц, затем – вверх на 1 единицу.

И т.д. Некоторые геометрические преобразования можно поменять местами, но это возможно далеко не всегда! Поэтому «чайникам» лучше придерживаться алгоритма, изложенного в начале параграфа.

Весь материал статьи, который носит в бОльшей степени всё-таки справочный характер, потребуется для выполнения чертежей в других задачах, но время от времени на практике рассматриваемое задание встречается отдельно, причём, бывает, в «сыром» виде:

Пример 20

Построить график функции  с помощью преобразований графиков элементарных функций

Методику быстрого построения параболы я разобрал на первом уроке о графиках функций, однако здесь по условию необходимо применить вполне определённый способ.

На первом шаге представим функцию в виде . Для этого используем так называемый метод выделения полного квадрата. Советую не пренебрегать задачей, поскольку типовой приём потребуется и в будущем, например, при нахождении интегралов от некоторых дробей.

Идея состоит в том, чтобы искусственно преобразовать функцию ТАК, чтобы воспользоваться одной из формул сокращенного умножения  либо .

Начнём преобразования. Коэффициент при  выносим за скобку:
Очевидно, что выражение сведётся к формуле . В скобках конструируем :
Таким образом, . Теперь организуем , для этого в скобках прибавим и вычтем :
Последнее слагаемое выносим из скобок:
Используем формулу  и суммируем два последних слагаемых:

В целях проверки целесообразно раскрыть скобки и убедиться, что получится исходная функция: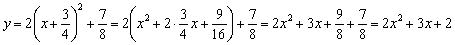

Построим график . Параболу :

1) Сдвинем вдоль оси  на  влево:  (синий цвет);
2) Вытянем вдоль оси  в 2 раза:  (малиновый цвет);
3) Сдвинем вдоль оси  на  вверх:  (красный цвет):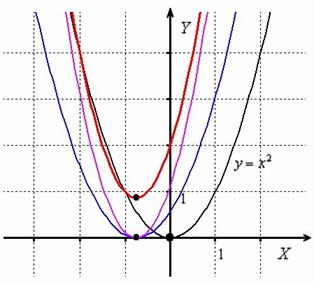

Рассмотрим ещё один типовой трюк:

Пример 21

Построить график функции  с помощью преобразований графиков элементарных функций.

Сначала сведём функцию к виду . Все действия я закомментирую: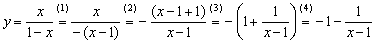

(1) В знаменателе выносим –1 за скобки. Это необходимо, чтобы аргумент функции представить «в привычном» порядке .
(2) Минус знаменателя поставим перед дробью. В числителе проведём искусственное преобразование – прибавим и вычтем единицу. Это необходимо для почленного деления на следующем шаге.
(3) Почленно делим числитель на знаменатель. Возьмите на заметку рассмотренный приём, он используется при интегрировании дробей.
(4) Раскрываем скобки.

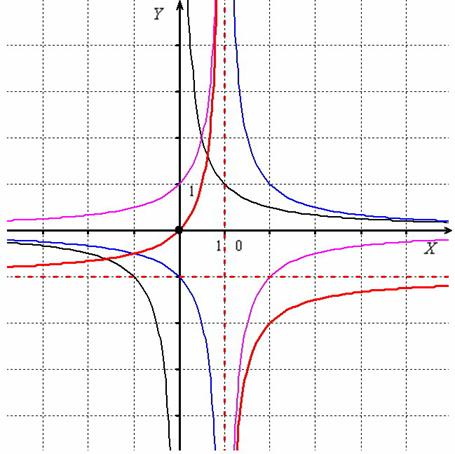
Проведём построение. График гиперболы  (чёрный цвет):

1) Сдвинем вправо на 1 единицу:  (синий цвет);
2) Отобразим симметрично относительно оси абсцисс:  (малиновый цвет);
3) Сдвинем вдоль оси  на единицу вниз:  (красный цвет):

Перейдём к заключительной части урока, в которой речь пойдёт о модуле. Хотел её сделать отдельной небольшой страничкой или pdf-кой, да потом передумал, чего уж тут мелочиться. Хотя эта статья далеко не рекордная по количеству букв, солидную часть объема занимают чертежи.

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

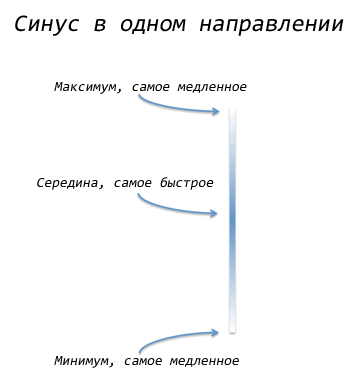
Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

• Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
• Спустя 1 секунду, вы прошли 10% от одной стороны
• Спустя 5 секунд, вы прошли одну сторону на 50%
• Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

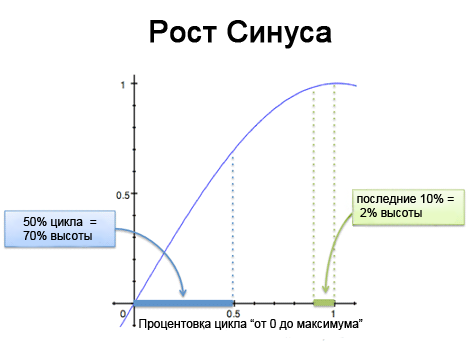
• Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
• Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
• И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

• Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
• Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?