Функция рост в excel
Содержание:
- Способ 3: интерполяция графика с помощью функции
- Из чего состоит временной ряд
- Виды моделей временного ряда
- Линейный регрессионный анализ
- Примеры как использовать
- Шаг 5
- Примеры использования функции СЕГОДНЯ в Excel
- #4. СРЗНАЧ
- #3. МИН
- Шаг 2
- Составляющие прогноза
- Информационные функции
- Пример функции ПРЕДСКАЗ в Excel
- Быстрый анализ в Excel
- Особенности использования функции КОРРЕЛ в Excel
- Особенности использования функции СЕГОДНЯ в Excel
- Прогнозирование будущих значений в Excel по условию
- Пример функции ПРЕДСКАЗ в Excel
- Шаг 2
- Функция РОСТ
- Возможно, у вас есть тренд
- Из чего состоит временной ряд
Способ 3: интерполяция графика с помощью функции
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
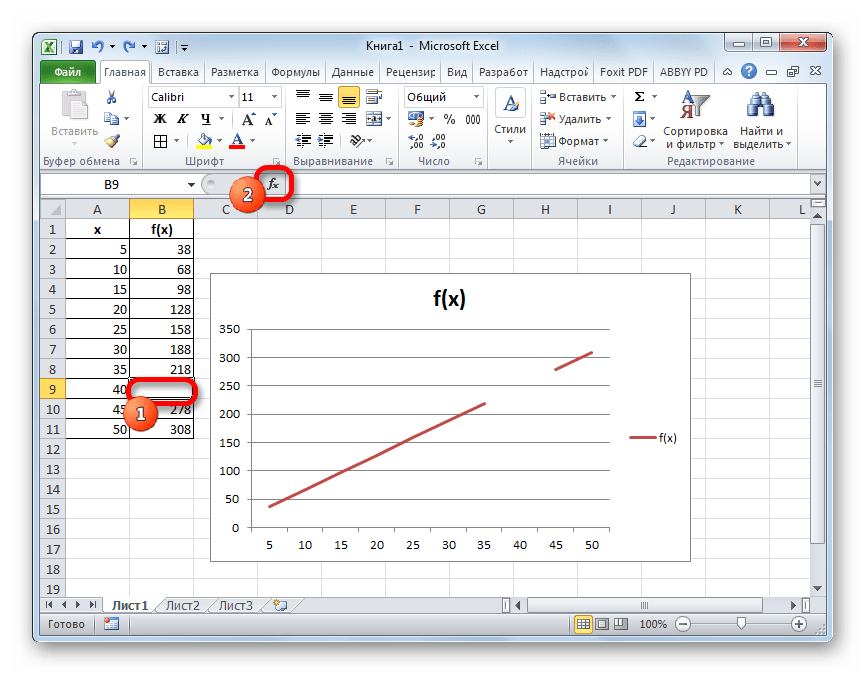
Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
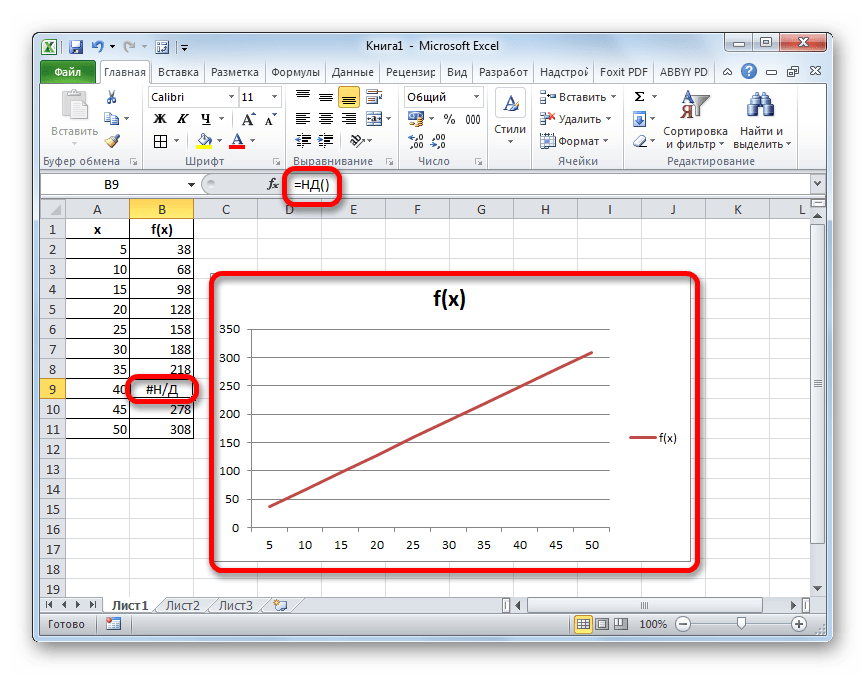
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
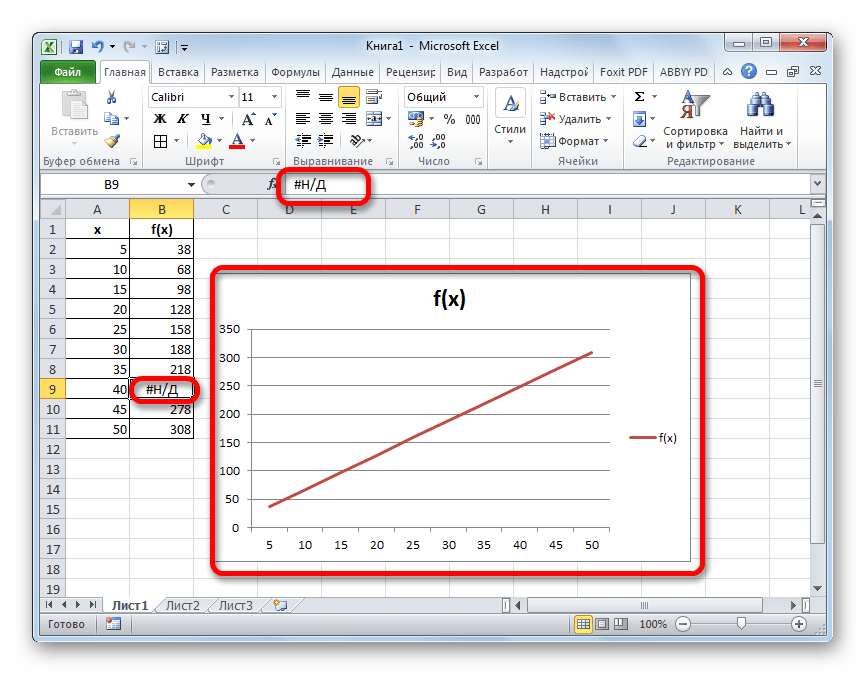
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.
Виды моделей временного ряда
Обычно, выделяют две модели временного ряда и третью — смешанную.
- Аддитивная модель
Мультипликативная модель 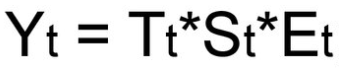
Смешанная модель 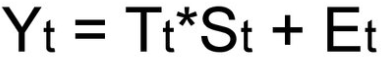
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:
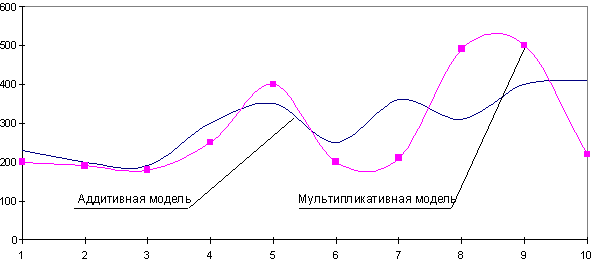
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).
Линейный регрессионный анализ
Выделяют несколько разновидностей регрессий: линейная, гиперболическая, множественная, логарифмически линейная, нелинейная, обратная, парная.
В рамках данной статьи мы рассмотрим линейную регрессию. В общем виде ее функция выглядит так:
В данном уравнении:
- Y – переменная, влияние на которую нужно найти;
- X – факторы, влияющие на переменную;
- A – коэффициенты регрессии, определяющие значимости факторов;
- N – общее количество факторов.
Чтобы было понятнее, давайте разберем конкретный практический пример. Допустим, у нас есть таблица, в которой представлена информация по среднесуточной температуре и количеству осадков с разбивкой по месяцам.

Наша задача – выяснить, как температура влияет на осадки. Приступи к ее выполнению.
- Щелкаем по кнопке “Анализ данных”.
- В открывшемся окошке отмечаем пункт “Регрессия”, после чего щелкаем OK.
- Перед нами появится окно, в котором нужно настроить параметры регрессии:
- в поле “Входной интервал_Y” пишем координаты диапазона ячеек, в которых находятся переменные, влияние на которые нам нужно выяснить. У нас это столбец “Количество осадков, мм”. Координаты диапазона можно указать как вручную, используя клавиши на клавиатуре, так и выделив его в самой таблице с помощью зажатой левой кнопки мыши.
- в поле “Входной интервал_X” указываем координаты диапазона ячеек с данными, влияние которых нам нужно найти. В нашем случае – это столбец “Среднесуточная температура”.
- Остальные параметры не являются обязательными и, чаще всего, остаются незаполненными. У нас есть возможность установить метки, значения уровня надежности в процентах, константу-ноль, график нормальной вероятности и т.д. Пожалуй, самым важным здесь является способ вывода результатов анализа. Доступны следующие варианты: на новом листе (по умолчанию), в новой книге или в указанном диапазоне на этом же листе. Мы оставим все как есть и жмем кнопку OK.
Примеры как использовать
Как известно, любую функцию в таблицу можно вставить тремя способами:
1. Через специального мастера с выполнением последовательно двух шагов.

2. Через строку формул.

3. Сразу в ячейке через знак равно.

Рассмотри несколько примеров:
1. Необходимо посчитать возраст сотрудников на данный момент, зная даты рождения. Записываете в ячейку формулу =ГОД(СЕГОДНЯ())-ГОД(C3), где ГОД возвращает только годовую часть даты, а затем при помощи маркера автозаполнения применяете выражение ко всей таблице.

Чтобы решить эту задачу, необходимо использовать специальную функцию ДЕНЬНЕД с аргументом СЕГОДНЯ
При этом важно правильно выбрать тип числа. Для того, чтобы понедельник был единицей, а воскресенье семеркой, нужно использовать второй тип

3. Рассмотрим, как делать минус дни от текущего момента.
Формула выглядит вот так:
=СЕГОДНЯ()-2, т.е. будет результат в виде даты без двух дней. Точно также работает и увеличение даты.


Как видите, самостоятельно функция СЕГОДНЯ используется редко. Однако в сочетании с другими формулами и с несколькими условиями функциональность выражения резко возрастает.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Шаг 5
Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

yi — спрогнозированные уровни ряда,
yi* — фактические уровни ряда,
n — количество складываемых элементов.
Модель может считаться адекватной, если:
Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.
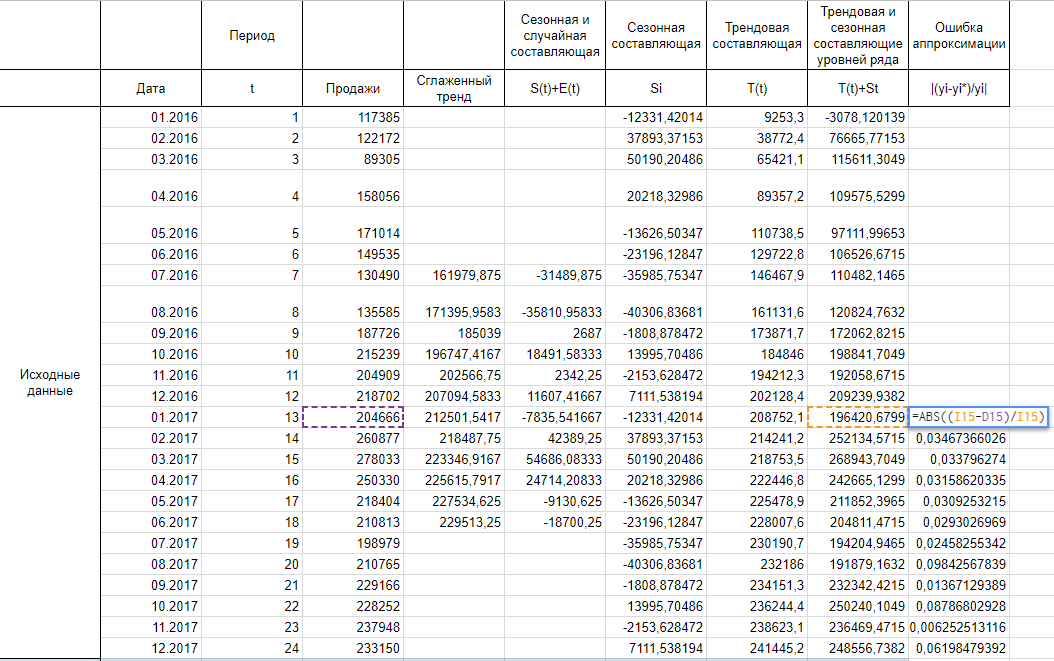
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.
Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении
Полезные ссылки:
- Ссылка на пример Google Sheets
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
- Бывшев В.А. Эконометрика
Екатерина Шипова
Магистр прикладной математики и информатики, веб-аналитик. Сертифицированный специалист Google Аnalytics и Яндекс.Метрика.
- Прогнозирование продаж в Excel с учетом сезонности — 27.06.2018
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности — 05.06.2018
- Когортный анализ. Сколько пользователей к вам вернулось? — 24.05.2018
Примеры использования функции СЕГОДНЯ в Excel
Пример 1. Компания ведет учет данных о своих сотрудниках и хранит соответствующие данные в таблицах Excel. В одной из таблиц хранятся даты рождения сотрудников. Необходимо добавить столбец, в котором будут отображаться динамически обновляемые данные о текущем возрасте сотрудников.
Исходная таблица данных:
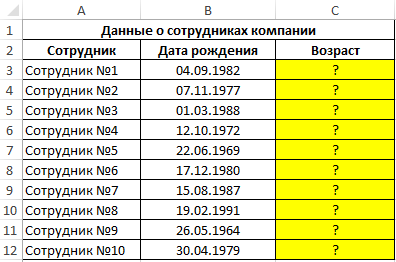
Определим возраст первого сотрудника с помощью следующей формулы:
Функция ГОД возвращает числовое значение года из указанной даты. Например, запись ГОД(СЕГОДНЯ()) вернет значение 2018, а ГОД(B3) – 1982. Для корректного отображения результатов необходимо отформатировать ячейки С3:C12 в Числовой формат. Результаты вычислений для всех сотрудников:
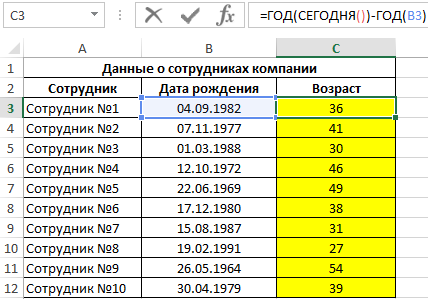
В отличие от ручного способа ввода текущего возраста сотрудника, представленные выше данные будут автоматически обновляться.
#4. СРЗНАЧ
Синтаксис: =СРЗНАЧ(число1;;…)
число1 — обязательный аргумент.
С помощью этой функции можно найти среднее арифметическое отдельных числовых значений, диапазонов, ссылок на ячейки с числовыми значениями или же среднее этих 3-х видов. Вычисляется путем суммирования всех чисел и делением суммы на количество этих же чисел. Текстовые и логические значения в диапазоне игнорируются.
Допустим, у нас есть диапазон из 6 ячеек: 4 из них заполнены числами, включая 0, одно значение — текстовое и еще одно — пустое. Функция просуммирует только числовые и поделит сумму на общее количество числовых — 4.
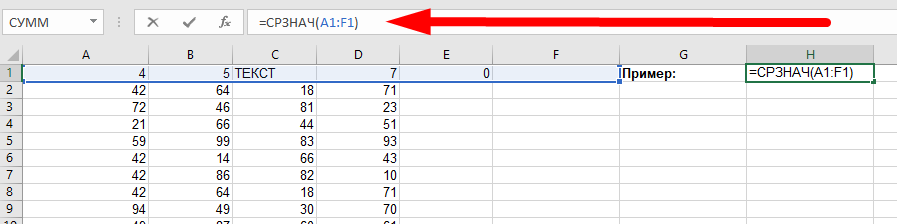
В результате мы получим среднее, равное 4. Давайте проверим формулой:
(4 + 5 + ТЕКСТ + 7 + 0 + ПУСТОЕ) / 4 = 16 / 4 = 4
ТЕКСТ и ПУСТОЕ игнорируются.
#3. МИН
Синтаксис: =МИН(число1;;…)
число1 — обязательный аргумент.
Функция позволяет найти минимальное числовое значение в указанном списке аргументов. Часто используется при построении финансовой отчетности, когда нужно определить дату начала периода отчета, минимальный чек покупки и другие параметры.
Пример
Допустим, у нас есть диапазон чисел и текстовых выражений, и нужно найти минимальное значение.
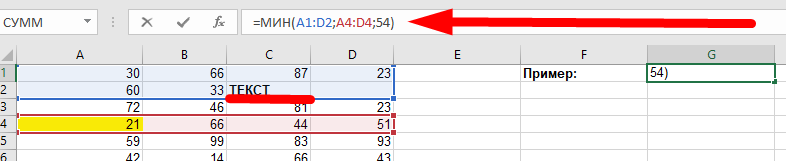
Например, минимальное значение среди двух выбранных диапазонов A1:D2, A4:D4 и числа 54 будет 21. Пустые поля и текстовые выражения функцией исключаются и в расчетах не используются.
Близкие по назначению функции
=МИНА(значение1;;…) — находит минимальное значение в списке аргументов, при этом текстовые и ложные логические выражения равняются к нулю, а логическое выражение «ИСТИНА» в ячейке равняется 1.
=МАКС(число1;;…) — находит максимальное значение в списке аргументов, при этом текстовые и пустые выражения игнорируются.
=МАКСА(значение1;;…) — находит максимальное значение в списке аргументов, при этом текстовые и ложные логические выражения приравниваются к нулю, а логическое выражение «ИСТИНА» в ячейке равняется 1.
Шаг 2
Так как мы рассматриваем аддитивную модель вида:
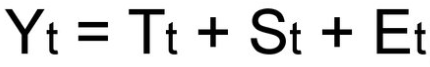
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.
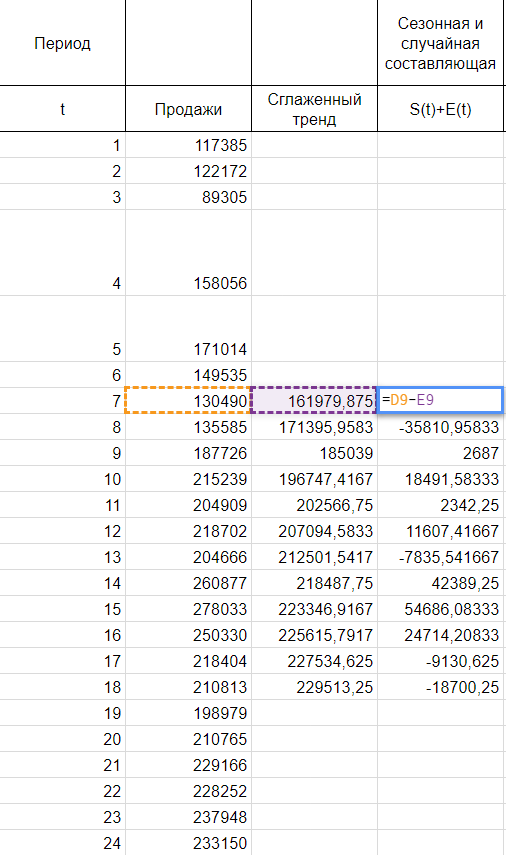
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:
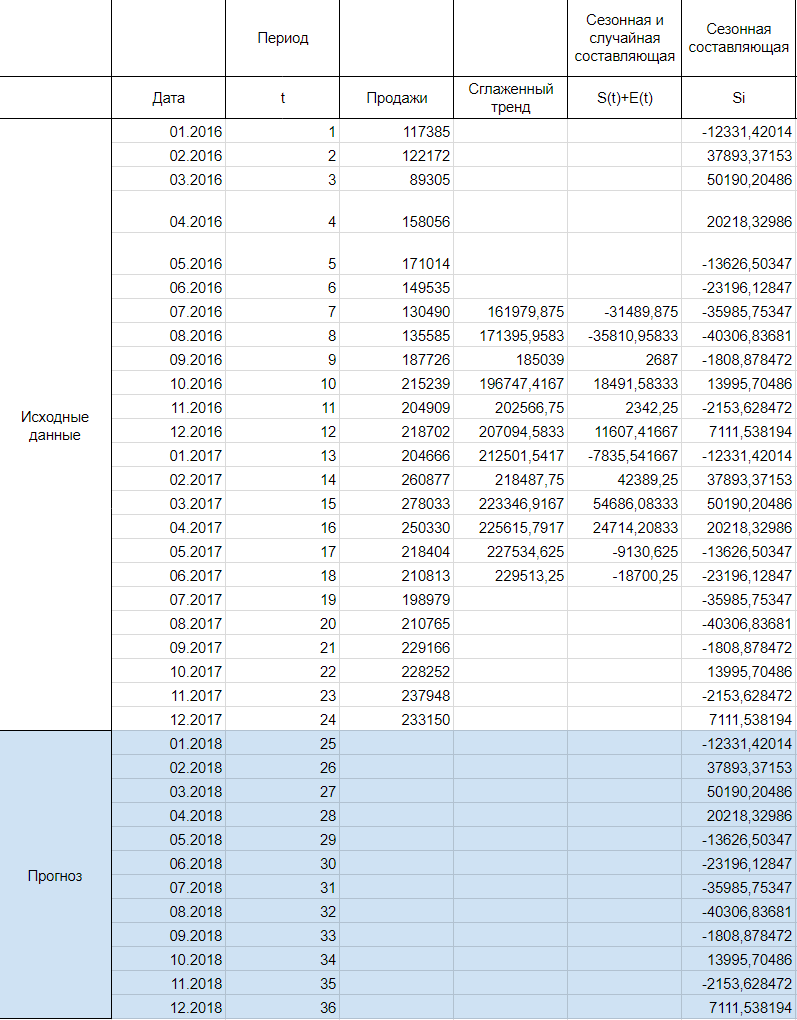
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно — продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Информационные функции
Данные формулы в основном являются средством для анализа данных. Прописать их довольно просто. Их назначение следующее:
- ЕПУСТО – проверка ячейки на наличие какого-нибудь значения;
- ЕНД – проверка ячейки на наличие ошибки #Н/Д;
- ЕЧИСЛО – проверка значения на соответствие числовому формату;
- ЕОШИБКА – проверка на наличие любой ошибки;
- ЕТЕКСТ – функция выдает истину, если в аргументе указано текстовое значение;
- ЕНЕТЕКСТ – аналогичная проверка, только наоборот;
- ЕОШ – функция вернет истинный результат, если в ячейке будет любая ошибка, отличная от #Н/Д;
- для проверки четного или нечетного значения используются формулы ЕЧЁТН и ЕНЕЧЁТ;
- ЕФОРМУЛА – проверка на наличие формулы в указанной ячейке.
Но есть и более сложная функция, о которой стоит поговорить отдельно.
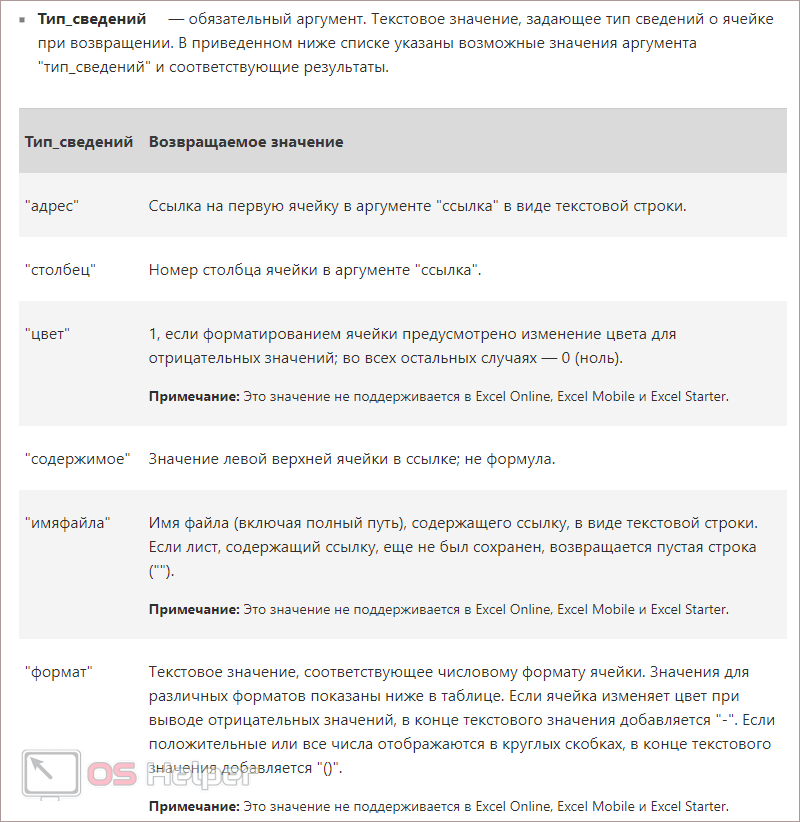
ЯЧЕЙКА
Используя этот инструмент, вы сможете узнать всю нужную информацию об указанной клетке. При этом необходимо использовать обязательный параметр – «Тип сведений», при помощи которого вы сможете узнать:
- цвет;
- адрес;
- столбец;
- тип;
- и многое другое.

Пример функции ПРЕДСКАЗ в Excel
Сначала возьмем для примера условные цифры – значения x и y.
В свободную ячейку введем формулу: =ПРЕДСКАЗ(31;A2:A6;B2:B6). Функция находит значение y для заданного значения x = 31. Результат – 20,9063.
Воспользуемся функцией для прогнозирования будущих продаж в Excel.
Сначала построим график по имеющимся данным.
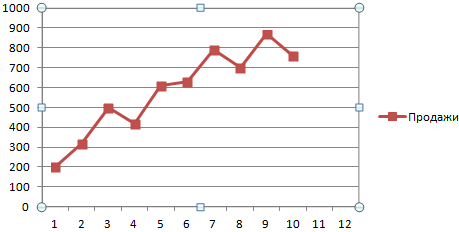
Выделим график. Щелкнем правой кнопкой мыши – «Добавить линию тренда». В появившемся окне установим галочки напротив пунктов «Показывать уравнение» и «Поместить величину достоверности аппроксимации».
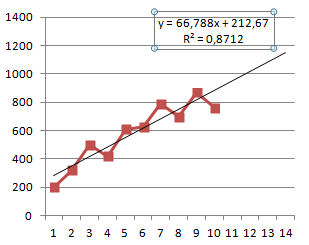
Линия тренда призвана показывать тенденцию изменения данных. Мы ее немного продолжили, чтобы увидеть значения за пределами заданных фактических диапазонов. То есть спрогнозировали. На графике просматривается четкая тенденция к росту будущих продаж в течение следующих двух месяцев.
Для расчета будущих продаж можно использовать уравнение, которое появилось на графике при добавлении линейного тренда. Его же мы используем для проверки работы функции ПРЕДСКАЗ, которая должна дать тот же результат.
Подставим значение x (11 месяц) в уравнение. Получим значение y (продажи для искомого месяца). Скопируем формулу до конца второго столбца.
Теперь для расчета будущих продаж воспользуемся функцией ПРЕДСКАЗ. Точка x, для которой необходимо рассчитать значение y, соответствует номеру месяца для прогнозирования (в нашем примере – ссылка на ячейку со значением 11 – А12). Формула: =ПРЕДСКАЗ(A12;$B$2:$B$11;$A$2:$A$11).
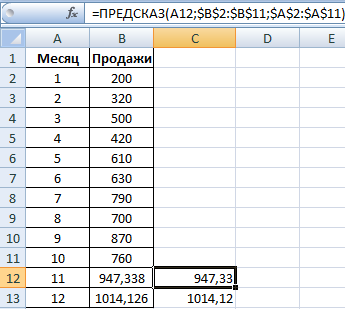
Абсолютные ссылки на диапазоны со значениями y и x делают их статичными (не позволяют изменяться, когда мы протягиваем формулу вниз).
Таким образом, для прогнозирования будущих значений на основе имеющихся фактических данных можно использовать функцию ПРЕДСКАЗ в Excel. Она входит в группу статистических функций и позволяет легко получить прогноз параметра y для заданного x.
Быстрый анализ в Excel
Предыдущий способ действительно хорош, потому что позволяет составлять реальные прогнозы, основываясь на статистических показателях. Но этот метод позволяет фактически проводить полноценную бизнес-аналитику. Очень классно, что эта возможность создана максимально эргономичной, поскольку для достижения желаемого результата необходимо совершить буквально несколько действий. Никаких ручных подсчетов, записи каких-либо формул. Достаточно просто выбрать диапазон, который будет анализироваться и задать конечную цель.
Как работать
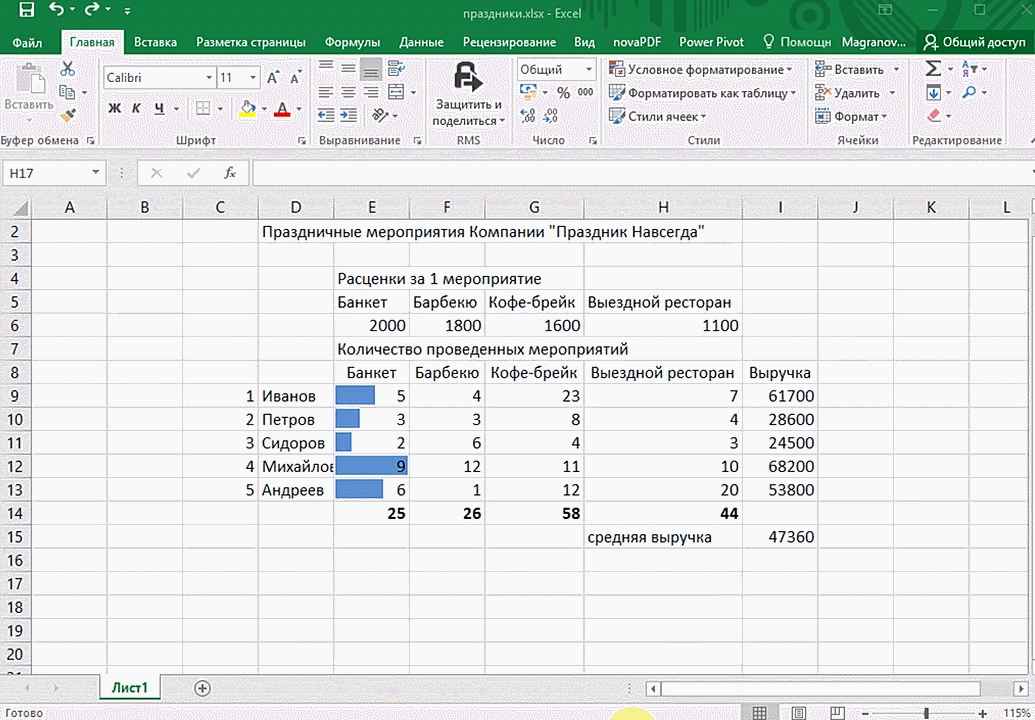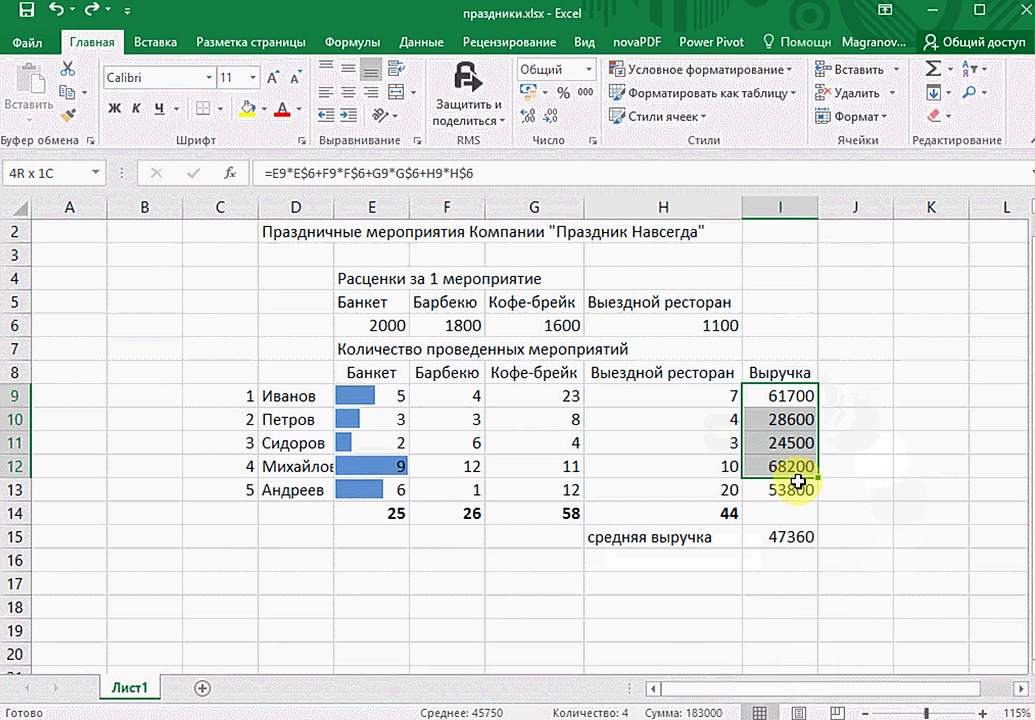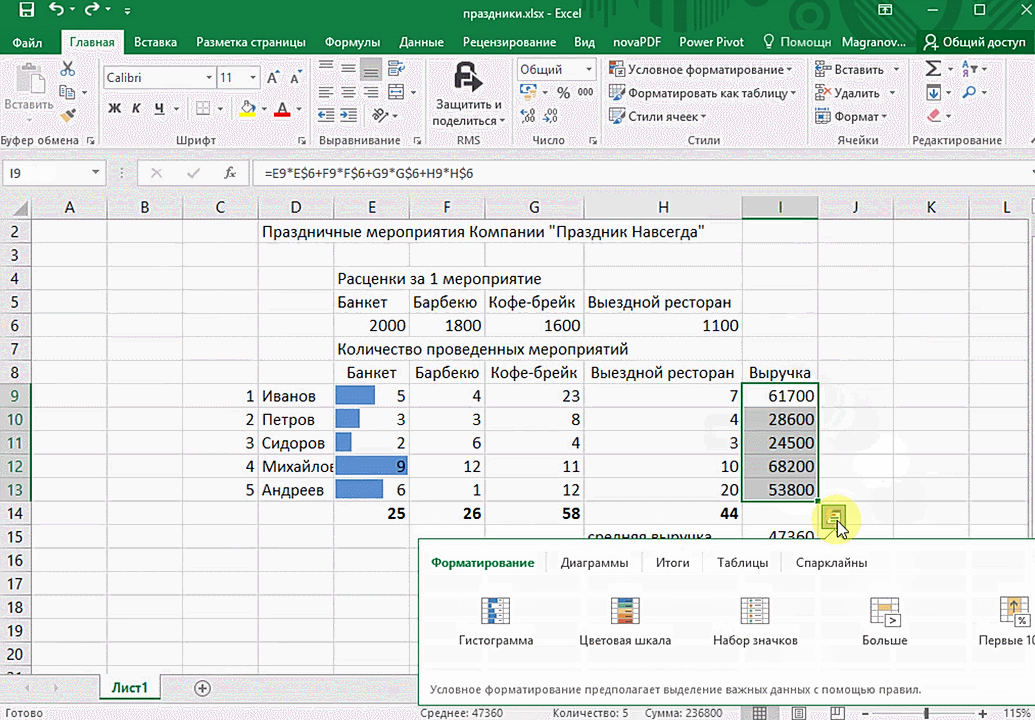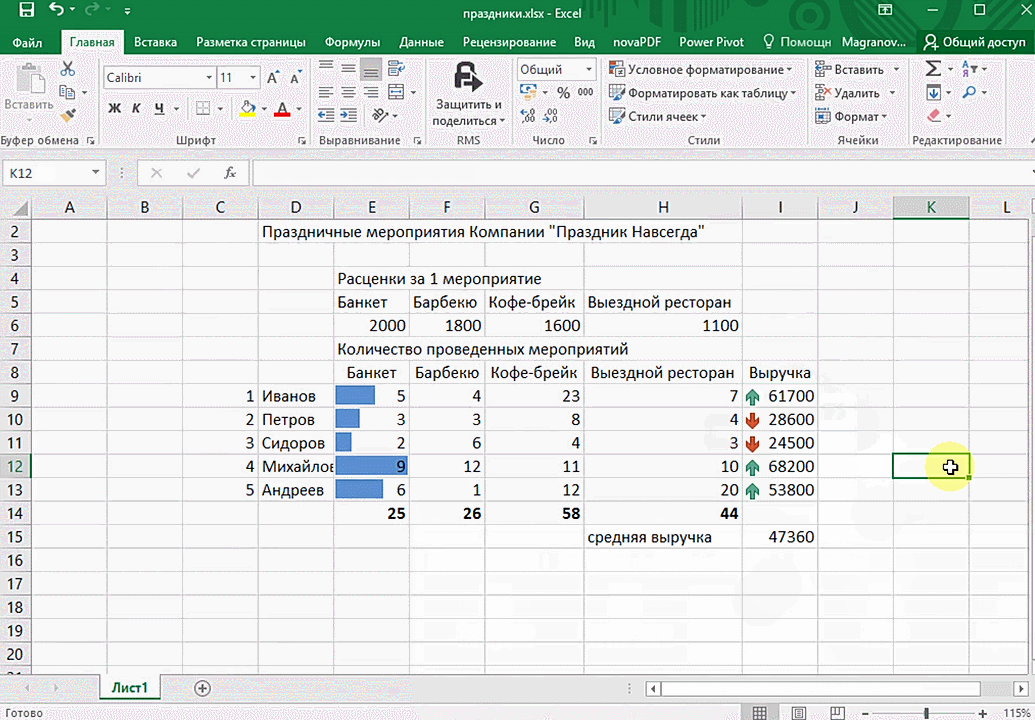
Итак, чтобы работать, нам надо надо открыть файл, в котором содержится тот набор данных, который надо анализировать и выделить соответствующий диапазон. После того, как мы его выделим, у нас автоматически появится кнопка, дающая возможность составить итоги или же выполнить набор других действий. Называется она быстрым анализом. Также мы можем определить суммы, которые автоматически будут проставлены внизу. Более наглядно посмотреть, как это работает, можете на этой анимации.
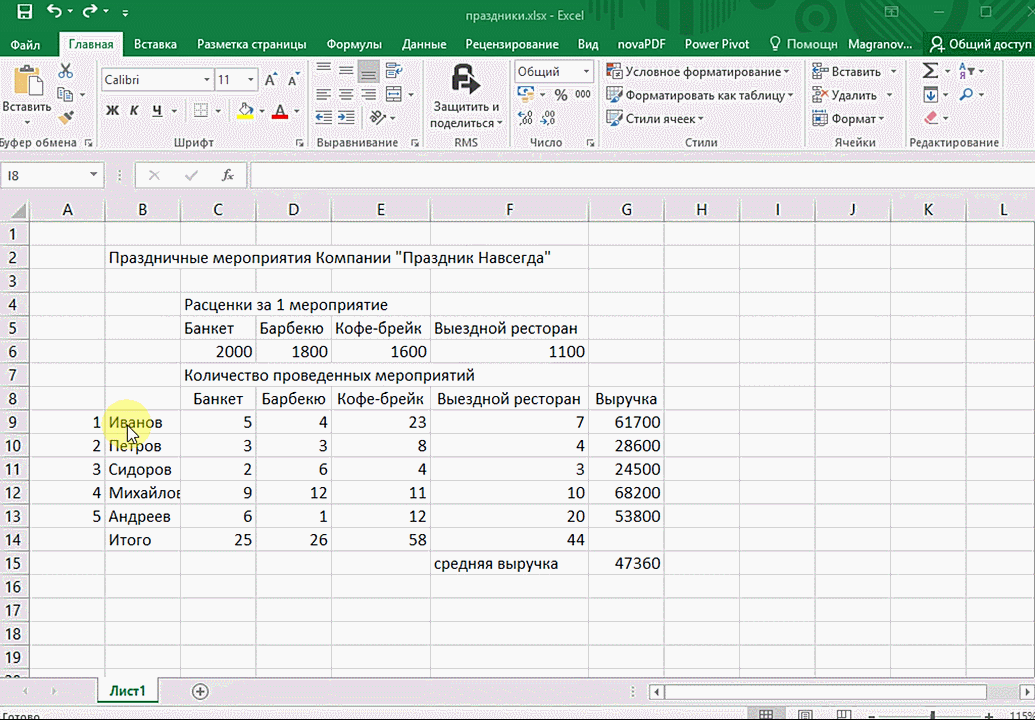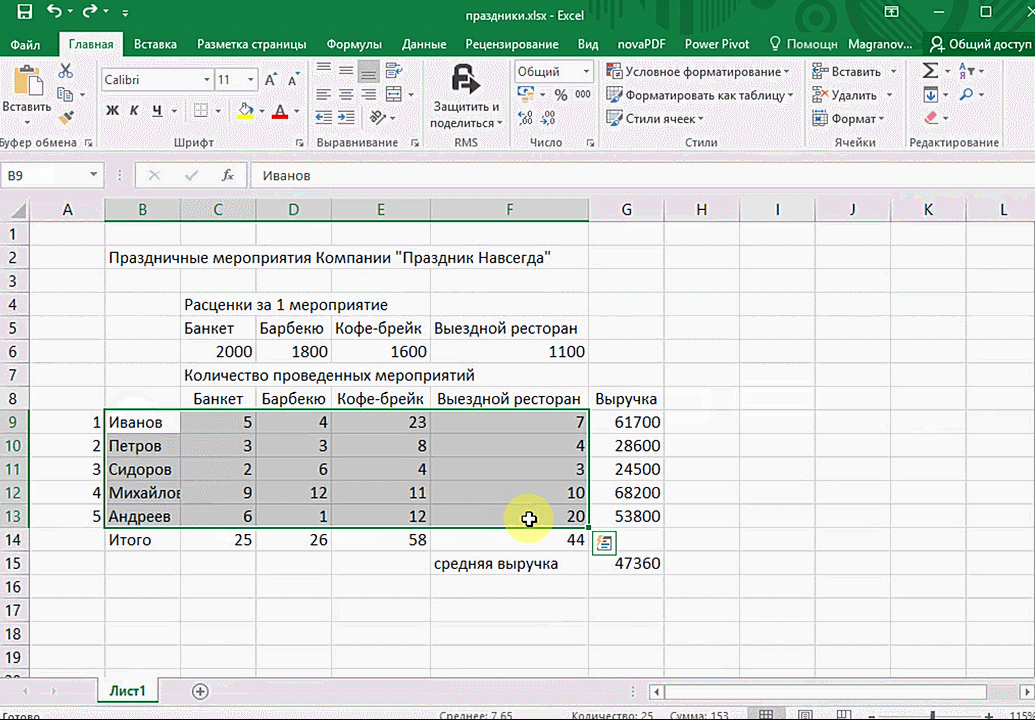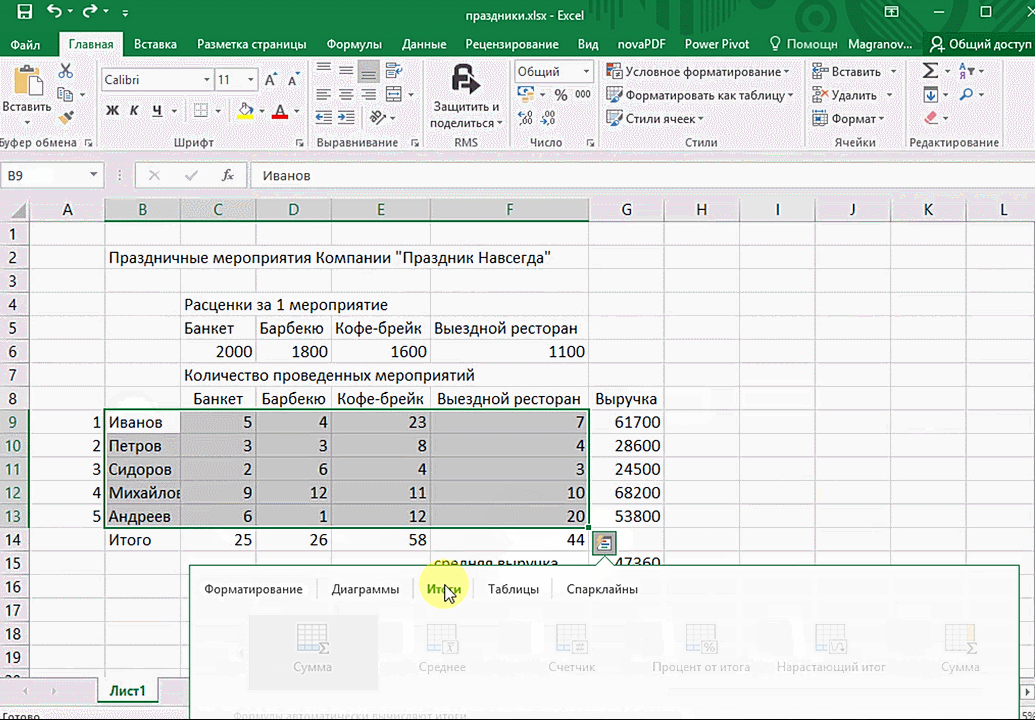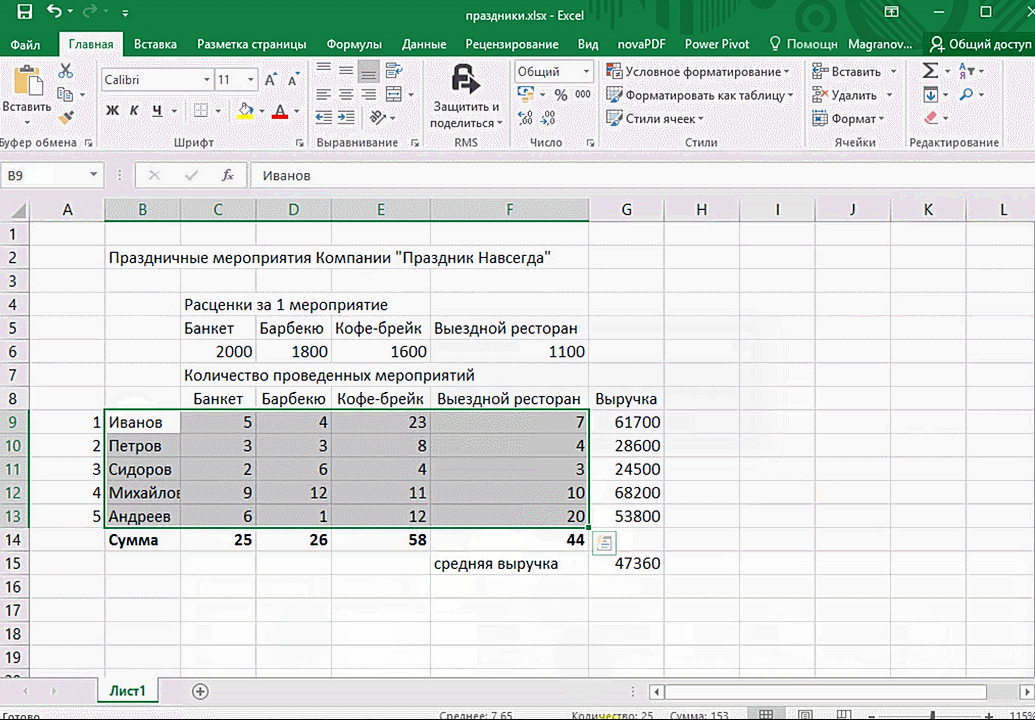
Функция быстрого анализа позволяет также по-разному форматировать получившиеся данные. А определить, какие значения больше или меньше, можно непосредственно в ячейках гистограммы, которая появляется после того, как мы настроим этот инструмент. 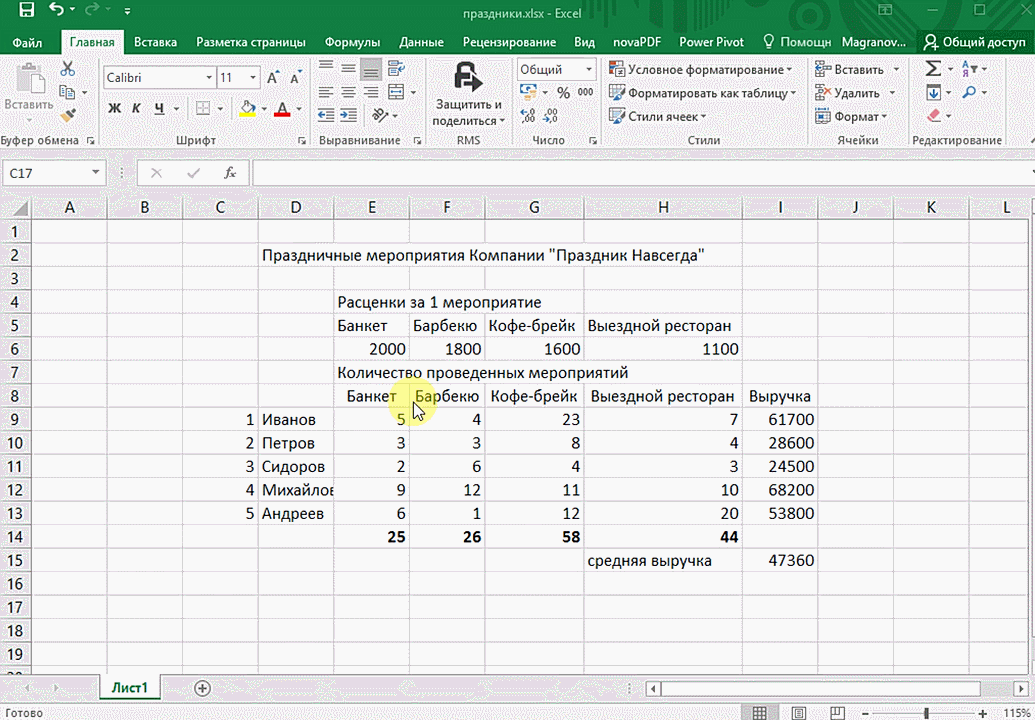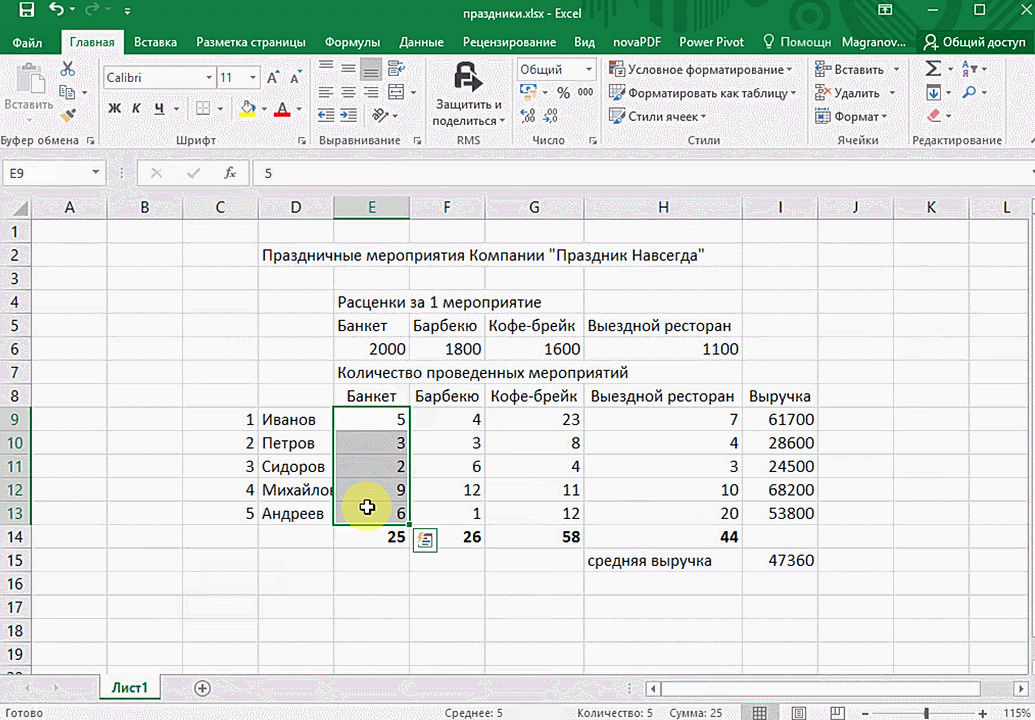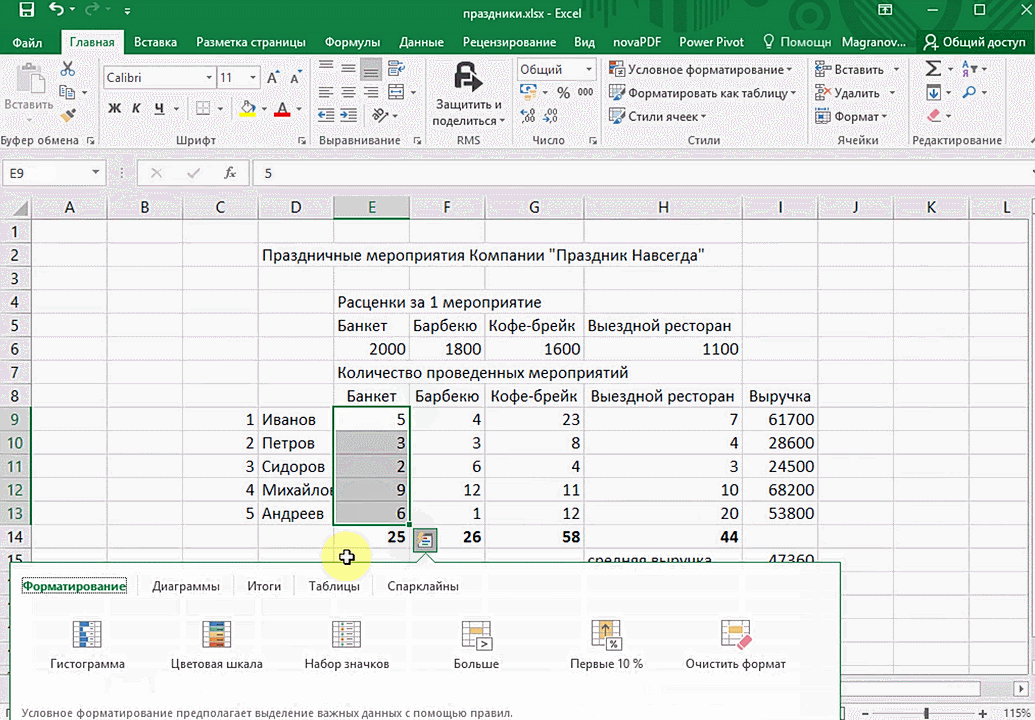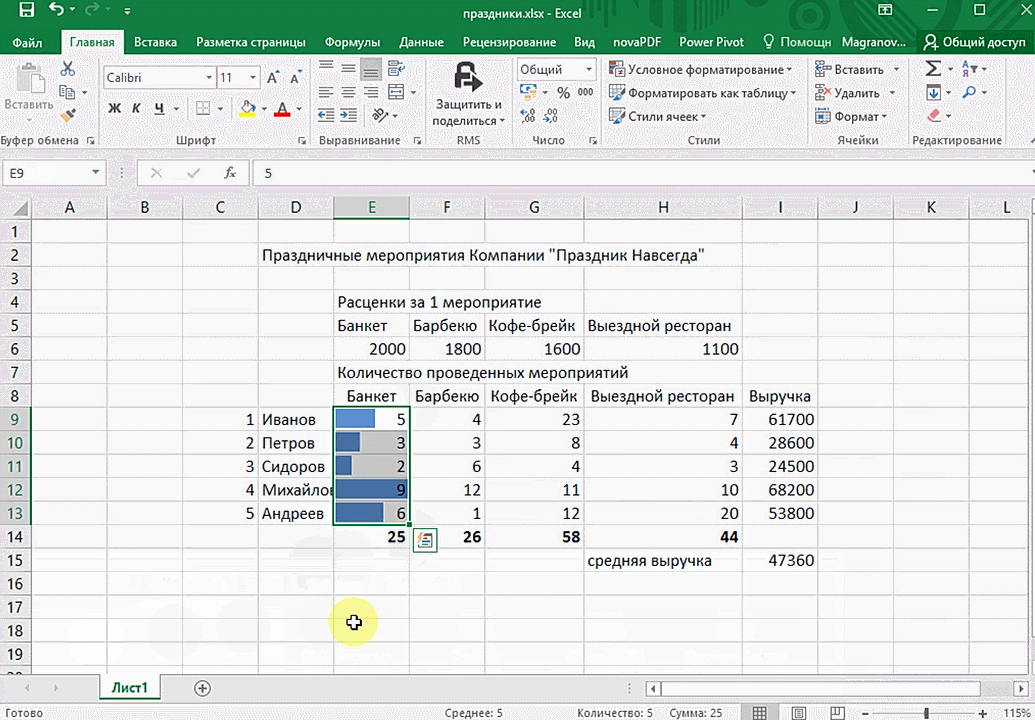
Также пользователь может поставить самые разные маркеры, которые обозначают большие и меньшие значения относительно тех, которые есть в выборке. Так, зеленым цветом будут показываться самые большие значения, а красным – наиболее маленькие.
Очень хочется верить, что эти приемы позволят вам значительно повысить эффективность вашей работы с электронными таблицами и максимально быстро добиться всего, что вы желаете. Как видим, эта программа для работы с электронными таблицами дает очень широкие возможности даже в стандартном функционале. А что уже говорить про дополнения, которых очень много на просторах интернета
Важно только обратить внимание, что все аддоны должны быть тщательно проверены на вирусы, потому что модули, написанные другими людьми, могут содержать вредоносный код. Если же надстройки разработаны компанией Майкрософт, то ее можно использовать смело
Пакет анализа от Майкрософт – очень функциональная надстройка, которая делает пользователя настоящим профессионалом. Она позволяет выполнить почти любую обработку количественных данных, но она довольно сложная для начинающего пользователя. На официальном сайте справки Майкрософт есть детальная инструкция по тому, как использовать разные виды анализа с помощью этого пакета.
Особенности использования функции КОРРЕЛ в Excel
Функция КОРРЕЛ имеет следующий синтаксис:
- массив1 – обязательный аргумент, содержащий диапазон ячеек или массив данных, которые характеризуют изменения свойства какого-либо объекта.
- массив2 – обязательный аргумент (диапазон ячеек либо массив), элементы которого характеризуют изменение свойств второго объекта.
- Функция КОРРЕЛ не учитывает в расчетах элементы массива или ячейки из выбранного диапазона, в которых содержатся данные текстового или логического типов. Пустые ячейки также игнорируются. Текстовые представления числовых значений учитываются.
- Если необходимо учесть логические ИСТИНА или ЛОЖЬ в качестве числовых значений 1 или 0 соответственно, можно выполнить явное преобразование данных используя двойное отрицание «–».
- Размерности массив1 и массив2 или количество ячеек, переданных в качестве этих двух аргументов, должны совпадать. Если аргументы содержат разное количество точек данных, например, =КОРРЕЛ(;), результатом выполнения функции будет код ошибки #Н/Д.
- Если один из аргументов представляет собой пустой массив или массив нулевых значений, функция КОРРЕЛ вернет код ошибки #ДЕЛ/0!. Аналогичный результат выполнения данной функции будет достигнут в случае, если стандартное отклонение распределения величин в одном из массивов (массив1, массив2) равно 0 (нулю).
- Функция КОРРЕЛ производит расчет коэффициента корреляции по следующей формуле:
Примечание 2: Коэффициент корреляции представляет собой количественную характеристику степени взаимосвязи между двумя свойствами объектов. Этот коэффициент может принимать значения из диапазона от -1 до 1, при этом:
- Если значение коэффициента приближается к 1 или -1, между двумя исследуемыми свойствами существует сильная прямая или обратная взаимосвязи соответственно.
- Если значение коэффициента стремится к 0,5 или -0,5, два свойства слабо прямо или обратно взаимосвязаны друг с другом соответственно.
- Если коэффициент корреляции близок к 0 (нулю), между двумя исследуемыми свойствами отсутствует прямая либо обратная взаимосвязи.
Примечание 3: Для понимания смысла коэффициента корреляции можно привести два простых примера:
- При нагреве вещества количество теплоты, содержащееся в нем, будет увеличиваться. То есть, между температурой и количеством теплоты (физическая величина) существует прямая взаимосвязь.
- При увеличении стоимости продукции спрос на нее уменьшается. То есть, между ценой и покупательной способностью существует обратная взаимосвязь.
Особенности использования функции СЕГОДНЯ в Excel
Функция имеет синтаксис без аргументов:
Данная функция не принимает аргументов.
- В Excel используется специальный формат представления дат для упрощения операций по расчету промежутков времени и дат. Excel работает с датами от 00.01.1900 (нулевой день был введен специально, поскольку отсчет начинается с нуля) до 31.12.9999, при этом каждая дата из данного промежутка представлена в виде количества дней, прошедших от начала отсчета – 00.01.1900.
- Если в результате выполнения функции СЕГОДНЯ требуется получить значение в форме записи дат, необходимо настроить соответствующий формат данных, отображаемых в ячейке. Если необходимо получить число в коде времени Excel, следует выбрать Числовой формат данных.
- Функция СЕГОДНЯ предоставляет динамически обновляемый результат в зависимости от даты открытия книги или обновления ее данных.
- Автоматическое обновление возвращаемого данной функцией результат может не происходить, если в пункте меню Параметры категории Формулы разделе Параметры вычислений не выбран вариант автоматического вычисления введенных формул.
- Данная функция сама по себе используется достаточно редко, однако часто применяется для вычисления разницы дат совместно с другими функциями для работы со временем и датами.
Прогнозирование будущих значений в Excel по условию
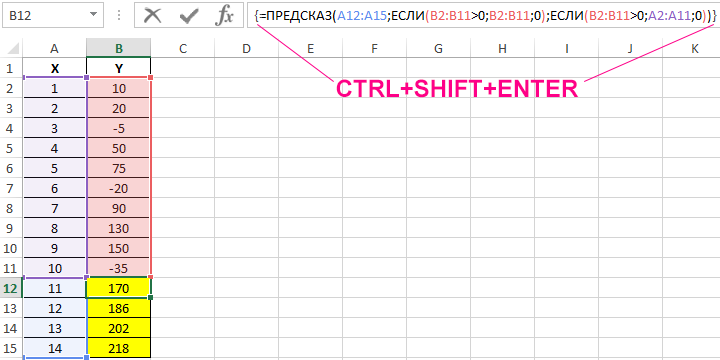
Пример 3. В таблице Excel указаны значения независимой и зависимой переменных. Некоторые значения зависимой переменной указаны в виде отрицательных чисел. Спрогнозировать несколько последующих значений зависимой переменной, исключив из расчетов отрицательные числа.
Вид таблицы данных:
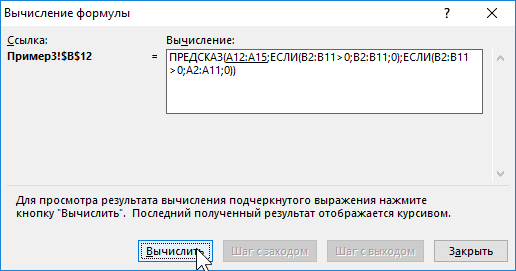
Для расчета будущих значений Y без учета отрицательных значений (-5, -20 и -35) используем формулу:
C помощью функций ЕСЛИ выполняется перебор элементов диапазона B2:B11 и отброс отрицательных чисел. Так, получаем прогнозные данные на основании значений в строках с номерами 2,3,5,6,8-10. Для детального анализа формулы выберите инструмент «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу». Один из этапов вычислений формулы:
Пример функции ПРЕДСКАЗ в Excel
Сначала возьмем для примера условные цифры – значения x и y.
В свободную ячейку введем формулу: =ПРЕДСКАЗ(31;A2:A6;B2:B6). Функция находит значение y для заданного значения x = 31. Результат – 20,9063.
Воспользуемся функцией для прогнозирования будущих продаж в Excel.
Сначала построим график по имеющимся данным.

Выделим график. Щелкнем правой кнопкой мыши – «Добавить линию тренда». В появившемся окне установим галочки напротив пунктов «Показывать уравнение» и «Поместить величину достоверности аппроксимации».

Линия тренда призвана показывать тенденцию изменения данных. Мы ее немного продолжили, чтобы увидеть значения за пределами заданных фактических диапазонов. То есть спрогнозировали. На графике просматривается четкая тенденция к росту будущих продаж в течение следующих двух месяцев.
Для расчета будущих продаж можно использовать уравнение, которое появилось на графике при добавлении линейного тренда. Его же мы используем для проверки работы функции ПРЕДСКАЗ, которая должна дать тот же результат.
Подставим значение x (11 месяц) в уравнение. Получим значение y (продажи для искомого месяца). Скопируем формулу до конца второго столбца.
Теперь для расчета будущих продаж воспользуемся функцией ПРЕДСКАЗ. Точка x, для которой необходимо рассчитать значение y, соответствует номеру месяца для прогнозирования (в нашем примере – ссылка на ячейку со значением 11 – А12). Формула: =ПРЕДСКАЗ(A12;$B$2:$B$11;$A$2:$A$11).

Абсолютные ссылки на диапазоны со значениями y и x делают их статичными (не позволяют изменяться, когда мы протягиваем формулу вниз).
Таким образом, для прогнозирования будущих значений на основе имеющихся фактических данных можно использовать функцию ПРЕДСКАЗ в Excel. Она входит в группу статистических функций и позволяет легко получить прогноз параметра y для заданного x.
Шаг 2
Так как мы рассматриваем аддитивную модель вида: 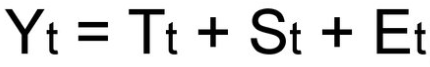
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.

Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:

Функция РОСТ
Дата добавления: 2013-12-23 ; просмотров: 9081 ; Нарушение авторских прав
ПРЕДСКАЗ(х; изв_знач_y; изв_знач_x)
Функция ПРЕДСКАЗ
Прогнозирование с помощью функций
Прогнозирование экономических показателей
Для расчета ожидаемого исполнения бюджета и при составлении проекта бюджета на следующий год используется прогнозирование различных экономических показателей.
В Excel для прогнозирования используются ряд функций (ПРЕДСКАЗ, РОСТ, ТЕНДЕНЦИЯ) и диаграммы.
Функция ПРЕДСКАЗ позволяет сделать прогноз, применяя линейную регрессию диапазона известных данных или массивов (x,y). Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по существующим значениям.
Предсказываемое значение — это y-значение, соответствующее заданному x-значению. Известные значения — это x- и y-значения, а новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для предсказания будущих продаж, потребностей в оборудовании или тенденций потребления.
х — это точка данных, для которой предсказывается значение.
изв_знач_y — это зависимый массив или интервал данных.
изв_знач_x — это независимый массив или интервал данных.
В качестве примера выполним расчет ожидаемой прибыли за 2006 год на основе данных о полученной прибыли в целом за год за 1999-2005 годы, используя функцию ПРЕДСКАЗ (рис. 92).
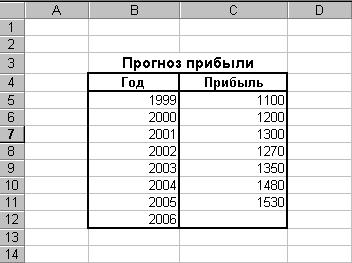
Рис. 92. Исходные данные для прогнозирования прибыли предприятия
Для расчета прибыли за 2006 год установите курсор в ячейку С12, выберите команду Функция в меню Вставка. В раскрывшемся окне Мастера функций выберите категориюфункцийСтатистическиеи затем вызовите функцию ПРЕДСКАЗ. На экране появится диалоговое окно функции ПРЕДСКАЗ. (рис. 93).
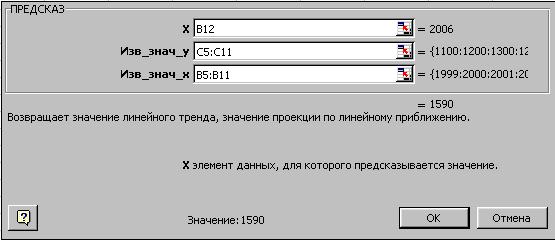
Рис. 93. Окно диалога функции ПРЕДСКАЗ
в появившемся окне введите исходные данные и получите результат (рис. 94).
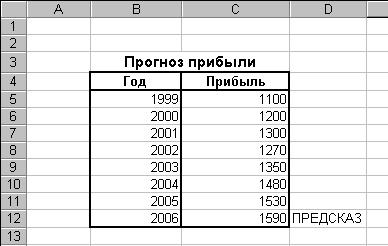
Рис. 94. Результаты прогнозирования с помощью функции ПРЕДСКАЗ
Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений. Функция рабочего листа РОСТ может применяться также для аппроксимации существующих x- и y-значений экспоненциальной кривой.
РОСТ(изв_знач_y; изв_знач_x; нов_знач_x; константа),
изв_знач_y — это множество значений y, которые уже известны для соотношения y = b*m^x.
изв_знач_x — это необязательное множество значений x, которые уже известны для соотношения y = b*m^x.
нов_знач_x — это новые значения x, для которых РОСТ возвращает соответствующие значения y.
константа — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1.
Если константа имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
Если константа имеет значение ЛОЖЬ, то b полагается равном 1, а значения m подбираются так, чтобы y = m^x.
В качестве примера использования этой функции выполним расчет прибыли за 2006 год на основе данных, приведенных на рис. 92.
Установите курсор в ячейку С12, выберите команду Функция в меню Вставка, а затем выберите функцию РОСТ. На экране появится диалоговое окно функции РОСТ (рис. 95).
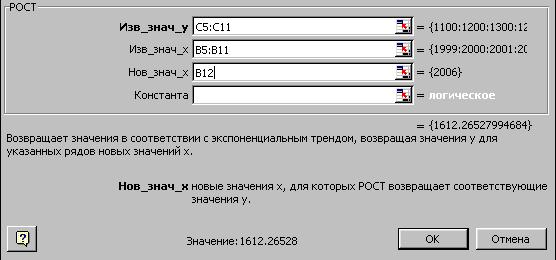
Рис. 95. Окно диалога функции РОСТ
в появившемся окне введите исходные данные и получите результат (рис. 96).
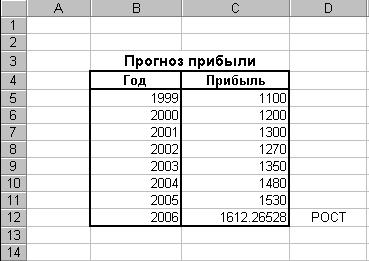
Рис. 96. Результаты прогнозирования с помощью функции РОСТ
Возможно, у вас есть тренд
Чтобы проверить это предположение достаточно подогнать линейную регрессию под данные спроса и выполнить тест на соответствие критерию Стьюдента на подъеме этой линии тренда (как в главе 6). Если уклон линии ненулевой и статистически значимый (в проверке по критерию Стьюдента величина р менее 0,05), у данных есть тренд (рис. 6).

Рис. 6. Тест Стьюдента показывает наличие тренда
Мы воспользовались функцией ЛИНЕЙН, которая возвращает 10 описательных статистик (если вы ранее не пользовались этой функцией, рекомендую Функция массива ЛИНЕЙН) и функцией ИНДЕКС, которая позволяет «вытащить» только три требуемые статистики, а не весь набор. Получилось, что наклон равен 2,54, и он значим, так как тест Стьюдента показал, 0,000000012 существенно меньше 0,05. Итак, тренд есть, и осталось включить его в прогноз.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.