Регрессия в excel

Использование Excel для определения линейной регрессии

Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа. Найти ее можно, перейдя по вкладке Файл –> Параметры (2007+), в появившемся диалоговом окне Параметры Excelпереходим во вкладку Надстройки. В поле Управление выбираем Надстройки Excelи щелкаем Перейти. В появившемся окне ставим галочку напротив Пакет анализа, жмем ОК.

Во вкладке Данные в группе Анализ появится новая кнопка Анализ данных.

Чтобы продемонстрировать работу надстройки, воспользуемся данными с предыдущей статьи, где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.

Перейдите во вкладку Данные, в группе Анализ щелкните Анализ данных. В появившемся окне Анализ данных выберите Регрессия, как показано на рисунке, и щелкните ОК.

Установите необходимыe параметры регрессии в окне Рег­рессия, как показано на рисунке:

Щелкните ОК. На рисунке ниже показаны полученные результаты:

Эти результаты соответствуют тем, которые мы получили путем самостоя­тельных вычислений в предыдущей статье.

Метод 1 Проверьте наличие возможности выполнить регрессивный анализ

1. Если в вашей версии Excel присутствует лента меню (Главная, Вставка, Разметка страницы, Формулы…):
   • Кликните на кнопку Office в верхней левой части страницы и перейдите в Параметры Excel.
   • Кликните на Надстройки в левой части страницы.
   • Найдите Analysis tool pack

     Если нужная строка указана в списке неактивных надстроек, в нижней части окна найдите строку Управление, убедитесь, что выбран пункт Надстройки Excel, и нажмите Перейти. В появившемся окне выберите Analysis tool pack и нажмите Оk. Разрешите установку, если потребуется.

     . Если это строка находится в списке активных надстроек, то все готово для работы.

2. Если в вашей версии Excel присутствует традиционное меню (Файл, Редактирование, Вид, Вставка…):
   • Перейдите в Инструменты > Надстройки.
   • Найдите Analysis tool pack. (Если этой строки нет, найдите ее, используя функцию Обзор

     Если нужная функция есть в поле Доступные надстройки, выберите опцию Analysis tool pack и нажмите Оk. Разрешите установку, если потребуется.

     .)

3. Excel для Mac 2011 и выше не поддерживает такой функционал. Соответственно, провести регрессивный анализ в Excel уже не получится; нужно искать другие программы. Почему так? Microsoft не очень любит Apple — конкуренты же.

Метод 2 Проводим регрессионный анализ

1. Введите в таблицу данные, которые будете анализировать. Вам нужно минимум 2 колонки с цифрами, которые будут символизировать входные интервалы Х и Y соответственно, где Y — зависимая переменная, а Х — независимая.

2. Откройте инструмент «Регрессионный анализ».
   • Для версий Excel с лентой: нажмите Данные» и в группе «Анализ» нажмите «Анализ данных» — «Регрессия».
   • Для версий Excel с обычным меню: нажмите Инструменты» — «Анализ данных» — «Регрессия».

3. Задайте входной интервал Y. В окне «Регрессия» кликните на Входной интервал Y, а затем выделите нужные ячейки. Вы увидите, как в поле появится соответствующая формула.

4. Задайте входной интервал Х аналогичным образом.

5. По желанию измените настройки. Выберите желаемые опции, отмечая соответствующие поля.

6. Определите, где будет показан результат анализа. Это может быть как отдельное место на рабочем листе, так и новый лист или новый файл.

7. Нажмите Оk. Результат анализа будет показан в выбранном вами месте.

Информация о статье

Эту страницу просматривали 23 267 раза.

Была ли эта статья полезной?

Линейная регрессия в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии

Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

В случае положительной корреляции при значении:

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

Основные задачи и виды регрессии

Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.

Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.

Основные задачи построения регрессионной модели заключаются в следующем:

1. Отбор значимых независимых переменных (Х1, Х2, …, Xk).
2. Выбор вида функции.
3. Построение оценок для коэффициентов.
4. Построение доверительных интервалов и функции регрессии.
5. Проверка значимости вычисленных оценок и построенного уравнения регрессии.

Регрессионный анализ бывает нескольких видов:

• парный (1 зависимая и 1 независимая переменные);
• множественный (несколько независимых переменных).

Уравнения регрессии бывает двух видов:

1. Линейные, иллюстрирующие строгую линейную связь между переменными.
2. Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.

Инструкция построения модели

Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL

1. Создайте файл исходных данных в MS Excel (например, таблица 2)

2. Построение корреляционного поля

Для построения корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма . В появившемся диалоговом окне выберите тип диаграммы: Точечная ; вид: Точечная диаграмма , позволяющая сравнить пары значений (Рис. 22).

Рисунок 22 – Выбор типа диаграммы

Рисунок 23– Вид окна при выборе диапазона и рядов Рисунок 25 – Вид окна, шаг 4

2. В контекстном меню выбираем команду Добавить линию тренда.

3. В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 26.

Нажимаем ОК. Результат представлен на рисунке 27.

Рисунок 27 – Корреляционное поле зависимости производительности труда от фондовооруженности

Аналогично строим корреляционное поле зависимости производительности труда от коэффициента сменности оборудования. (рисунок 28).

от коэффициента сменности оборудования

3. Построение корреляционной матрицы.

Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.

С помощью инструмента анализа данных Регрессия , помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки . Установите флажок Пакет анализа (Рисунок 29)

Рисунок 30 – Диалоговое окно Анализ данных

После нажатия ОК в появившемся диалоговом окне указываем входной интервал (в нашем примере А2:D26), группирование (в нашем случае по столбцам) и параметры вывода, как показано на рисунке 31.

Результат расчетов представлен в таблице 4.

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

1. Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
2. Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
3. Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
4. Жмем «Закрыть».

Теперь стали видны и данные регрессионного анализа.

Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:

ŷ = a + bx

где:

ŷ — ожидаемое значение у при заданном значении х,

x — независимая переменная,

a — отрезок на оси y для прямой линии,

b — наклон прямой линии.

На рисунке ниже это понятие представлено графически:

На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.

Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

ŷ = 2 + 0.5x

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4

Обратите внимание, что ожидаемое значение у в соответствии с линией при х = 2 является ŷ. Мы можем подтвердить это с помощью следу­ющего уравнения:

ŷ = 2 + 0.5х =2 +0.5(2) =3.

Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.

Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.

Вставка точечной диаграммы в Excel

Предположим, у вас есть два столбца данных в Excel, и вы хотите вставить точечную диаграмму, чтобы проверить взаимосвязь между этими двумя переменными.

Начните с выбора данных в двух столбцах. Затем нажмите на Вставить вкладка на лента и найдите Графики раздел. Нажмите на кнопку с надписью рассеивать а затем выберите кнопку из меню под названием Разброс только с маркерами,

В более новых версиях Excel точечные диаграммы будут отображаться в виде маленькой кнопки с графиком и точками, как показано ниже. Кроме того, вы выберете просто рассеивать из выпадающего списка.

Теперь у вас должен быть точечный график с вашими данными, представленными на графике.

Добавить линию тренда в Excel

Теперь, когда у вас есть график рассеяния на листе Excel, вы можете добавить свою линию тренда. Начните, нажав один раз на любую точку данных на графике рассеяния. Это может быть сложно, потому что есть много элементов диаграммы, которые вы можете щелкнуть и отредактировать.

Вы будете знать, что выбрали точку данных, когда выбраны все точки данных. Выбрав точки данных, щелкните правой кнопкой мыши любую точку данных и выберите Добавить линию тренда из меню.

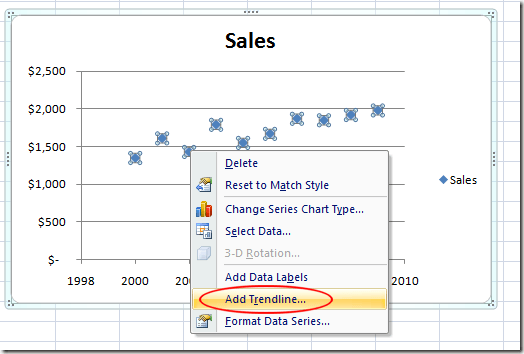
Теперь вы должны смотреть на Формат Trendline окно. Это окно содержит много опций для добавления линии тренда в график рассеяния Excel.

Обратите внимание, что вы можете добавить экспоненциальный, линейный, логарифмический, многочлен, Сила, или Скользящая средняя линия тренда / регрессии. Пока оставьте значение по умолчанию линейный опция выбрана

Нажмите на близко Кнопка и ваш график теперь должны отображать линию тренда линейной регрессии

Пока оставьте значение по умолчанию линейный опция выбрана. Нажмите на близко Кнопка и ваш график теперь должны отображать линию тренда линейной регрессии.

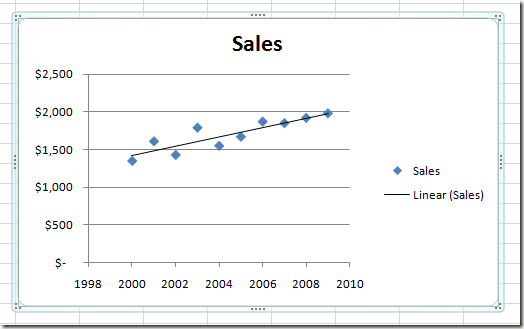
Как и во всех вещах Microsoft Office, вы можете отформатировать свою линию тренда так, чтобы она выглядела именно так, как вы хотите. В следующем разделе мы обсудим некоторые наиболее популярные изменения, которые вы можете внести в свою линию тренда, чтобы она выделялась.

Форматирование Excel Trendline

Чтобы отформатировать вновь созданную линию тренда, начните с щелчка правой кнопкой мыши по линии и выбора Формат Trendline из меню. Excel снова откроет Формат Trendline панель.

Один из наиболее популярных вариантов, которые люди используют при добавлении линии тренда в Excel, заключается в отображении как уравнения линии, так и значения R-квадрата прямо на графике. Вы можете найти и выбрать эти опции внизу окна. Пока выберите оба эти варианта.

Допустим, мы хотим, чтобы наша линия тренда отображалась более четко на графике. В конце концов, линия тренда по умолчанию имеет ширину всего в один пиксель и может иногда исчезать среди цветов и других элементов на графике. На левой стороне Формат Trendline нажмите на Fill & Line значок.

В этом окне измените ширина значение от 0,75 до примерно 3 и измените Тип тире к Квадратная точка вариант (третий в выпадающем меню). Просто чтобы продемонстрировать, что опция существует, измените Тип конца вариант со стрелкой.

Когда вы закончите, нажмите Икс кнопка на Формат Trendline панель и обратите внимание на изменения вашего точечного графика. Обратите внимание, что уравнение линии и значения R-квадрата теперь отображаются на графике и что линия тренда является более заметным элементом диаграммы

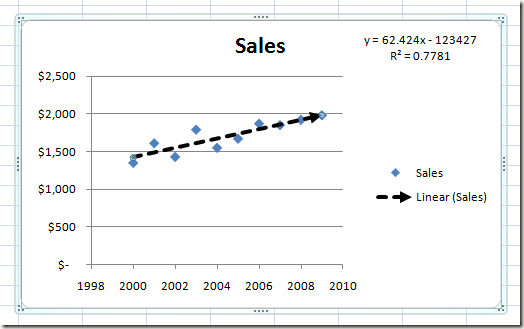
Как и многие функции в Excel, у вас есть практически безграничные опции, доступные вам при отображении линии тренда на диаграмме рассеяния.

Вы можете изменить цвет и толщину линии и даже добавить к ней 3D-элементы, такие как эффект затенения (нажмите на Последствия значок).

То, что вы выберете, зависит от того, насколько заметно вы хотите, чтобы ваша линия тренда выделялась на вашем графике. Поэкспериментируйте с опциями, и вы можете легко создать профессионально выглядящую линию тренда в Excel. Наслаждайтесь!

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

• линейной (у = а + bx);
• параболической (y = a + bx + cx2);
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а0 + а1х1 +…+акхк.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Сохранение шаблона диаграммы в Excel

Если созданный график действительно Вам нравится, то можно сохранить его в качестве шаблона (.crtx файла), а затем применять этот шаблон для создания других диаграмм в Excel.

Как создать шаблон диаграммы

В Excel 2013 и 2016, чтобы сохранить график в качестве шаблона, щелкните правой кнопкой мыши по диаграмме и в выпадающем меню выберите Сохранить как шаблон (Save as Template):

В Excel 2010 и более ранних версиях, функция Сохранить как шаблон (Save as Template) находится на Ленте меню на вкладке Конструктор (Design) в разделе Тип (Type).

После нажатия Сохранить как шаблон (Save as Template) появится диалоговое окно Сохранение шаблона диаграммы (Save Chart Template), где нужно ввести имя шаблона и нажать кнопку Сохранить (Save).

По умолчанию вновь созданный шаблон диаграммы сохраняется в специальную папку Charts. Все шаблоны диаграмм автоматически добавляются в раздел Шаблоны (Templates), который появляется в диалоговых окнах Вставка диаграммы (Insert Chart) и Изменение типа диаграммы (Change Chart Type) в Excel.

Имейте ввиду, что только те шаблоны, которые были сохранены в папке Charts будут доступны в разделе Шаблоны (Templates). Убедитесь, что не изменили папку по умолчанию при сохранении шаблона.

Совет: Если Вы загрузили шаблоны диаграмм из Интернета и хотите, чтобы они были доступны в Excel при создании графика, сохраните загруженный шаблон как .crtx файл в папке Charts:

Как использовать шаблон диаграммы

Чтобы создать диаграмму в Excel из шаблона, откройте диалоговое окно Вставка диаграммы (Insert Chart), нажав на кнопку Просмотр всех диаграмм (See All Charts) в правом нижнем углу раздела Диаграммы (Charts). На вкладке Все диаграммы (All Charts) перейдите в раздел Шаблоны (Templates) и среди доступных шаблонов выберите нужный.

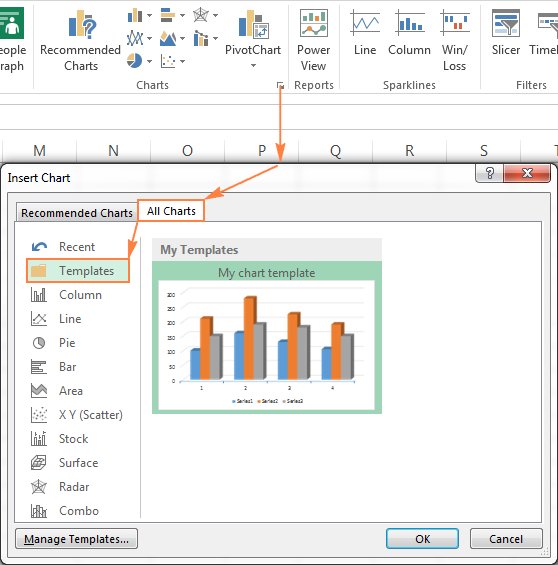
Чтобы применить шаблон диаграммы к уже созданной диаграмме, щелкните правой кнопкой мыши по диаграмме и в контекстном меню выберите Изменить тип диаграммы (Change Chart Type). Или перейдите на вкладку Конструктор (Design) и нажмите кнопку Изменить тип диаграммы (Change Chart Type) в разделе Тип (Type).

В обоих случаях откроется диалоговое окно Изменение типа диаграммы (Change Chart Type), где в разделе Шаблоны (Templates) можно выбрать нужный шаблон.

Как удалить шаблон диаграммы в Excel

Чтобы удалить шаблон диаграммы, откройте диалоговое окно Вставка диаграммы (Insert Chart), перейдите в раздел Шаблоны (Templates) и нажмите кнопку Управление шаблонами (Manage Templates) в левом нижнем углу.

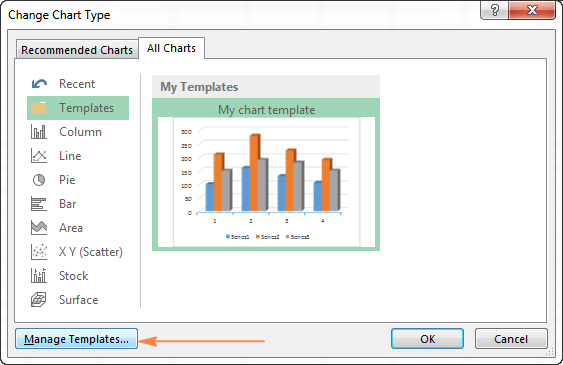
Нажатие кнопки Управление шаблонами (Manage Templates) откроет папку Charts, в которой содержатся все существующие шаблоны. Щелкните правой кнопкой мыши на шаблоне, который нужно удалить, и выберите Удалить (Delete) в контекстном меню.

Выполняем корреляционный анализ

Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.

Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.

Метод 1: применяем функцию КОРРЕЛ

В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:

Порядок действий при работе с данным инструментом следующий:

1. Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
2. В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
3. На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
4. Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.

Метод 2: используем “Пакет анализа”

Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:

1. Заходим в меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
4. В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.

Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:

1. Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
2. Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
3. На экране отобразится окно, в котором необходимо указать следующие параметры:
   • “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
   • “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
   • “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
   • Когда все готово, щелкаем OK.
4. Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.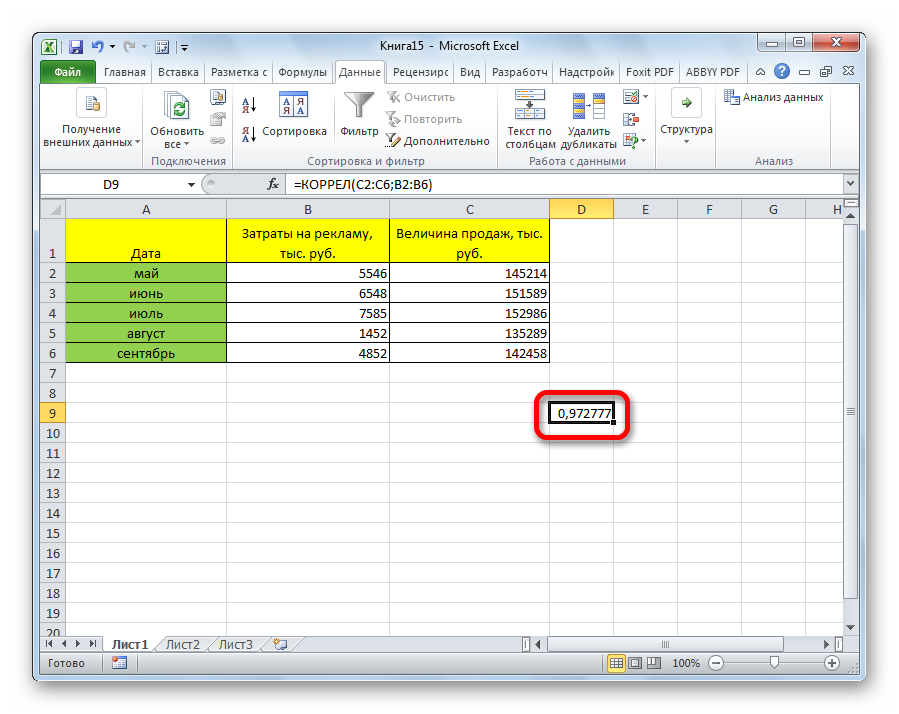 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.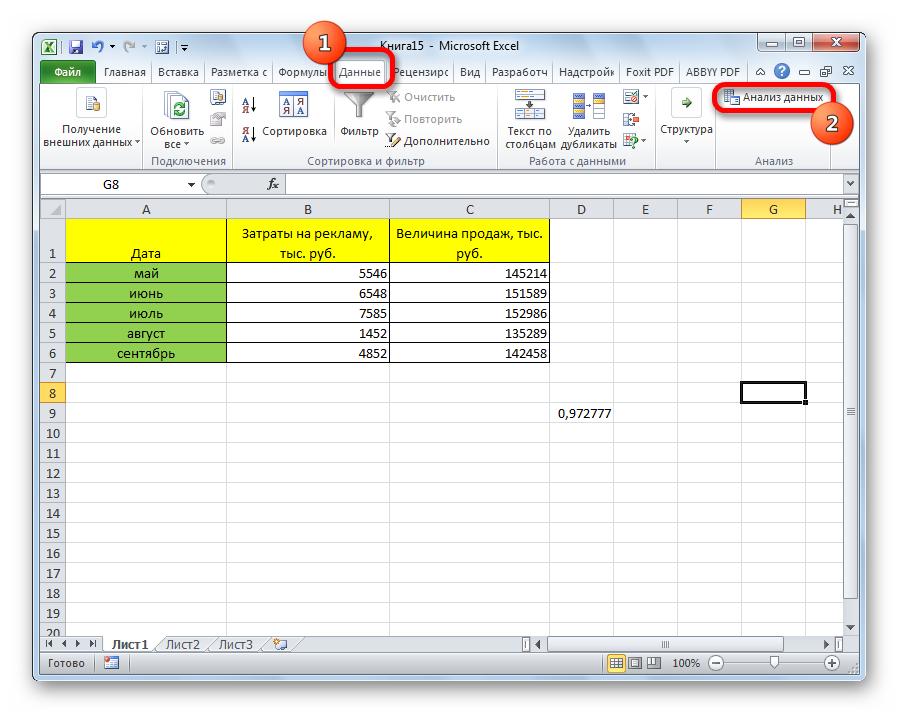 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.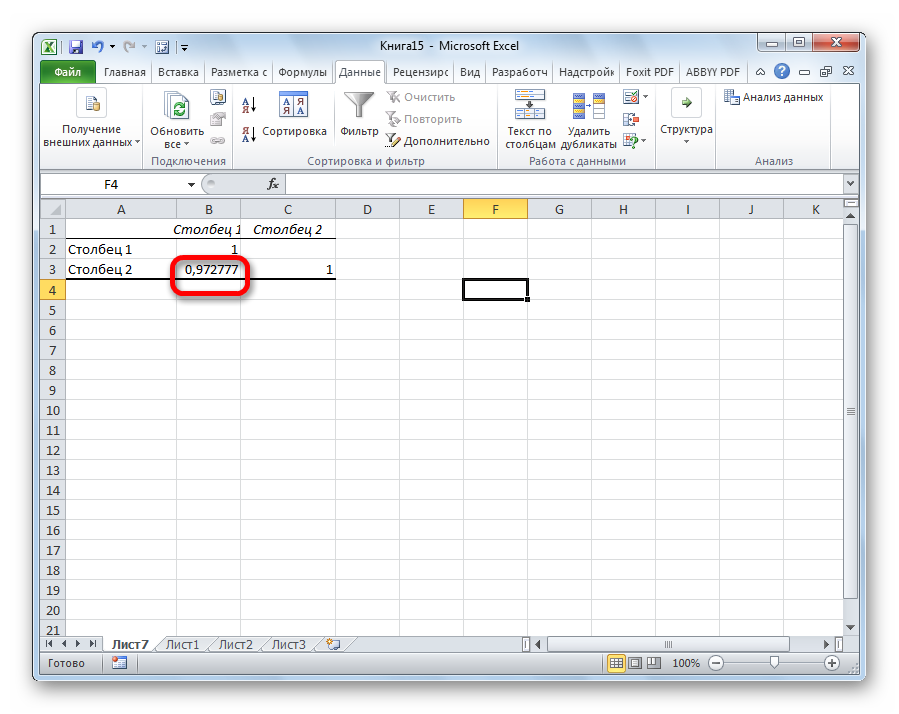 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х_i; Y_i). Для наглядности построим диаграмму рассеяния.

Примечание: Подробнее о построении диаграмм см. статью Основы построения диаграмм. В файле примера для построения диаграммы рассеяния использована диаграмма График, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

Расчеты корреляции проведем для различных случаев взаимосвязи между переменными: линейной, квадратичной и при отсутствии связи.

Примечание: В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

В файле примера для построения диаграммы рассеяния в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми. Как было сказано выше, для расчета коэффициента корреляции в MS EXCEL существует функций КОРРЕЛ()

Также можно воспользоваться аналогичной функцией PEARSON() , которая возвращает тот же результат

Как было сказано выше, для расчета коэффициента корреляции в MS EXCEL существует функций КОРРЕЛ() . Также можно воспользоваться аналогичной функцией PEARSON() , которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления корреляции производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычисление корреляции с помощью более подробных формул:

Примечание: Квадрат коэффициента корреляции r равен коэффициенту детерминации R2, который вычисляется при построении линии регрессии с помощью функции КВПИРСОН() . Значение R2 также можно вывести на диаграмме рассеяния, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку Макет, затем в группе Анализ нажмите кнопку Линия тренда и выберите Линейное приближение). Подробнее о построении линии тренда см., например, в статье о методе наименьших квадратов.