Как найти число зная среднее арифметическое

Занимательная математика. Среднее значение

В математике среднее арифметическое значение чисел (или просто среднее) — это сумма всех чисел в данном наборе, разделенная на их количество. Это наиболее обобщенное и распространенное понятие средней величины. Как вы уже поняли, чтобы найти среднее значение, нужно суммировать все данные вам числа, а полученный результат разделить на количество слагаемых.

Что такое среднее арифметическое?

Давайте рассмотрим пример.

Пример 1. Даны числа: 6, 7, 11. Нужно найти их среднее значение.

Решение.

Для начала найдем сумму всех данных чисел.

6 + 7 + 11 = 24

Теперь разделим получившуюся сумму на количество слагаемых. Так как у нас слагаемых три, соответственно, мы будем делить на три.

24 : 3 = 8

Следовательно, среднее значение чисел 6, 7 и 11 — это 8. Почему именно 8? Да потому, что сумма 6, 7 и 11 будет такая же, как трех восьмерок. Это отлично видно на иллюстрации.

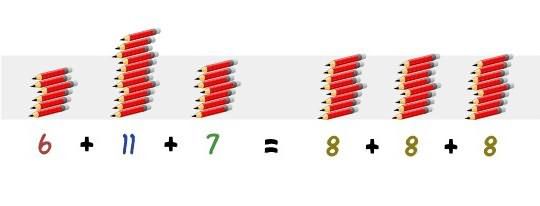
Среднее значение чем-то напоминает «выравнивание» ряда чисел. Как видите, кучки карандашей стали одного уровня.

Рассмотрим еще один пример, чтобы закрепить полученные знания.

Пример 2. Даны числа: 3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29. Нужно найти их среднее арифметическое значение.

Решение.

Находим сумму.

3 + 7 + 5 + 13 + 20 + 23 + 39 + 23 + 40 + 23 + 14 + 12 + 56 + 23 + 29 = 330

Делим на количество слагаемых (в этом случае — 15).

330 : 15 = 22

Следовательно, среднее значение данного ряда чисел равно 22.

Теперь рассмотрим отрицательные числа. Вспомним, как их суммировать. Например, у вас есть два числа 1 и -4. Найдем их сумму.

1 + (-4) = 1 – 4 = -3

Зная это, рассмотрим еще один пример.

Пример 3. Найти среднее значение ряда чисел: 3, -7, 5, 13, -2.

Решение.

Находим сумму чисел.

3 + (-7) + 5 + 13 + (-2) = 12

Так как слагаемых 5, разделим получившуюся сумму на 5.

12 : 5 = 2,4

Следовательно, среднее арифметическое значение чисел 3, -7, 5, 13, -2 равно 2,4.

Для того чтобы посчитать среднее значение ряда чисел, необходимо использовать функцию AVERAGE. Синтаксис для этой функции:
= Average (argument1, argument2, … argument255)
где argument1, argument2, … argument255 — это либо числа, либо ссылки на ячейки (под ячейками подразумеваются диапазоны и массивы).

Чтобы было более понятно, опробуем полученные знания.

1. Введите числа 11, 12, 13, 14, 15, 16 в ячейки С1 – С6.
2. Выделите ячейку С7, нажав на нее. В этой ячейке у нас будет отображаться среднее значение.
3. Щелкните на вкладке «Формулы».
4. Выберите More Functions > Statistical для того, чтобы открыть выпадающий список.
5. Выберите AVERAGE. После этого должно открыться диалоговое окно.
6. Выделите и перетащите туда ячейки С1–С6, чтобы задать диапазон в диалоговом окне.
7. Подтвердите свои действия клавишей «ОК».
8. Если вы все сделали правильно, в ячейке С7 у вас должен появиться ответ – 13,7. При нажатии на ячейку C7 функция (= Average (C1: C6)) будет отображаться в строке формул.

Очень удобно использовать эту функцию для ведения учета, накладных или когда вам просто нужно найти среднее значение из очень длинного ряда чисел. Поэтому ее часто используют в офисах и крупных компаниях. Это позволяет сохранять порядок в записях и дает возможность быстро посчитать что-либо (например, средний доход за месяц). Также с помощью Excel можно найти среднее значение функции.

fb.ru

Способ с помощью Мастера функций

Способов, позволяющих найти среднее арифметическое в Excel, существует много, и естественно, что с их помощью есть возможность обойти ограничения, предполагающие предыдущий способ. Сейчас будет рассказано о произведении вычислений путем использования Мастера функций. Итак, вот что вам необходимо сделать.

1. Нажав левую кнопку мыши, выделите ячейку, в которой хотите видеть результат вычислений.
2. Откройте окно Мастера функций, нажав по кнопке «Вставить функцию», расположенной слева от строки формул либо использовав горячие клавиши Shift+F3.
3. В появившемся окне отыщите в списке строку «СРЗНАЧ», выделите ее и нажмите кнопку «ОК».
4. Появится новое окно для ввода аргументов функции. В нем вы увидите два поля: «Число1» и «Число2».
5. В первое поле введите адреса ячеек, в которых расположены числовые значения для расчета. Сделать это можно как вручную, так и с помощью специального инструмента. Во втором случае нажмите по кнопке, расположенной в правой части поля для ввода. Окно Мастера свернется и вам необходимо будет выделить мышкой ячейки для расчета.
6. Если другой диапазон ячеек с данными находится в другом месте листа, тогда укажите его в поле «Число2».
7. Проделайте ввод данных, пока не укажете все необходимые.
8. Нажмите кнопку «ОК».

По завершении ввода окно Мастера закроется, а в ячейке, которую вы выделяли в самом начале, появится результат вычислений. Теперь вы знаете второй способ, как рассчитать среднее арифметическое в Excel. Но далеко не последний, поэтому двигаемся дальше.

Основная идея

Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:

Свободное место, допустим, только одно, и наша задача – выбрать достойного.

Первое, что обычно приходит в голову – это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ

На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется “Программирование”, а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень

Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение

Средневзвешенное – это среднее с учетом различной ценности (веса, важности) каждого из элементов. В бизнесе средневзвешенное часто используется в таких задачах, как:

В бизнесе средневзвешенное часто используется в таких задачах, как:

оценка портфеля акций, когда у каждой из них своя ценность/рисковость
оценка прогресса по проекту, когда у задач не равный вес и важность
оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
и т.д.

Расчет средневзвешенного формулами

Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е

среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:

Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах – оценки абитурента и вес каждого предмета – а затем суммирует все полученные произведения

Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость

Основные свойства средней арифметической

• Если индивидуальные значения признака (варианты), уменьшить (увеличить) в n раз, то среднее значение нового признака соответственно уменьшится или увеличится во столько же.
• Если все варианты осредняемого признака уменьшить (увеличить) на число А, то средняя арифметическая соответственно изменится на это же число.
• Если вес всех осредняемых вариантов уменьшить (увеличить) в k раз, то средняя арифметическая не изменится.
• Сумма отклонений отдельных значений признака от средней арифметической равна нулю.

Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака.

Вычисление с помощью Мастера функций

Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.

Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.

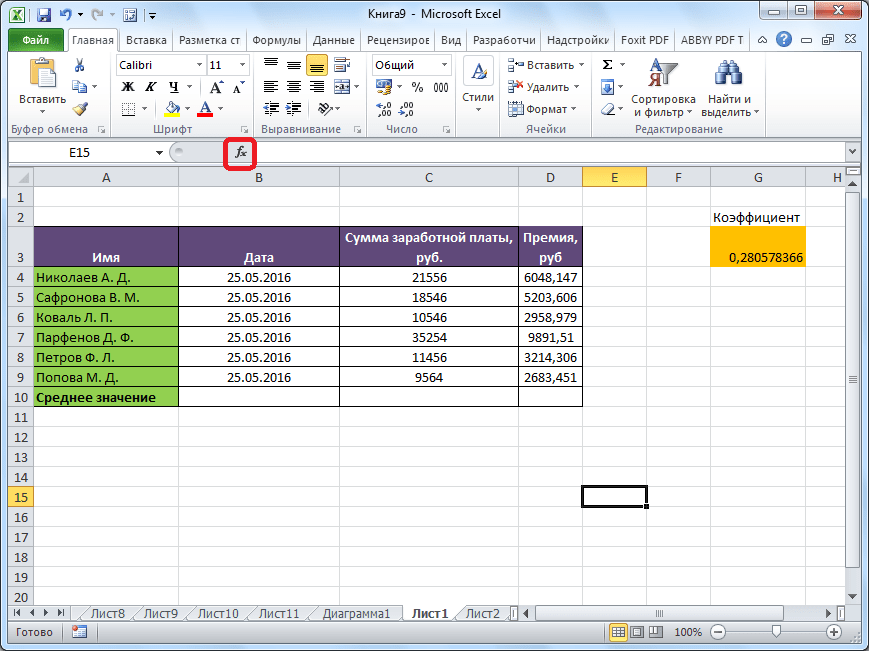
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».

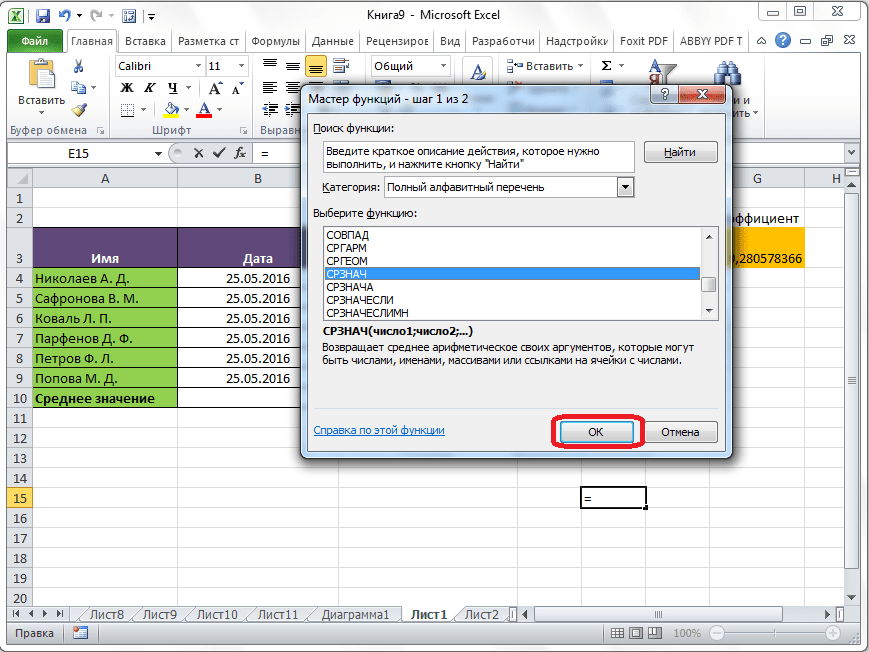
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.

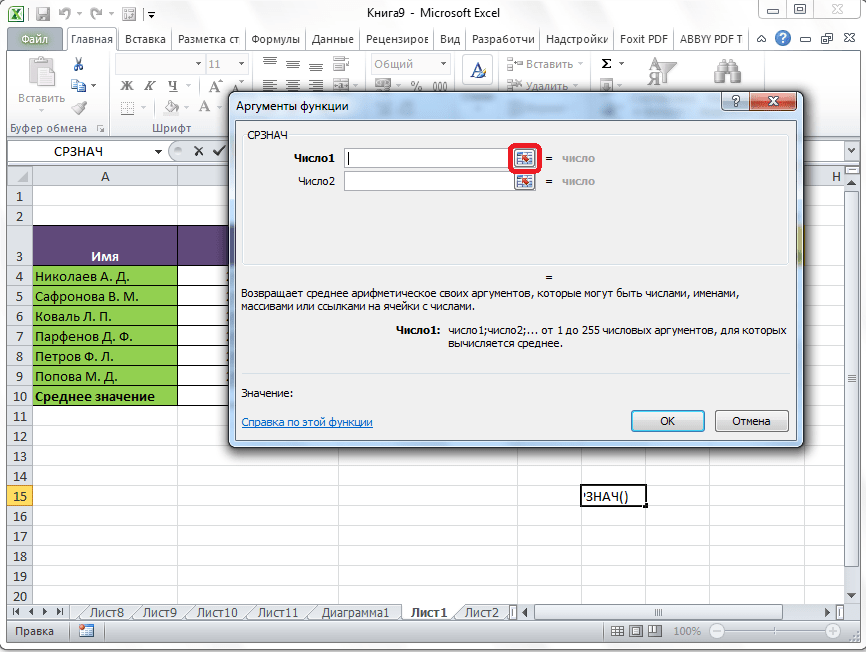
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.

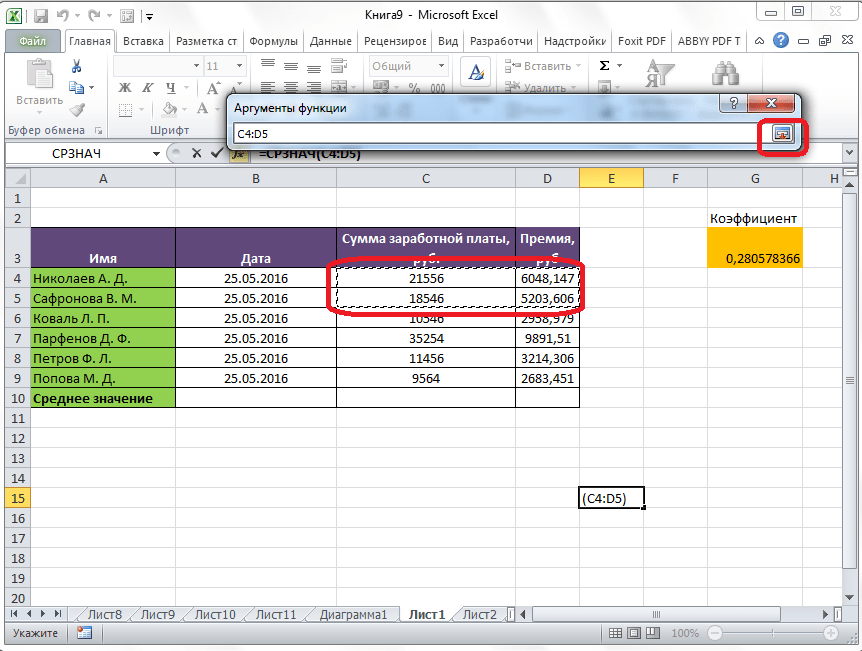
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.

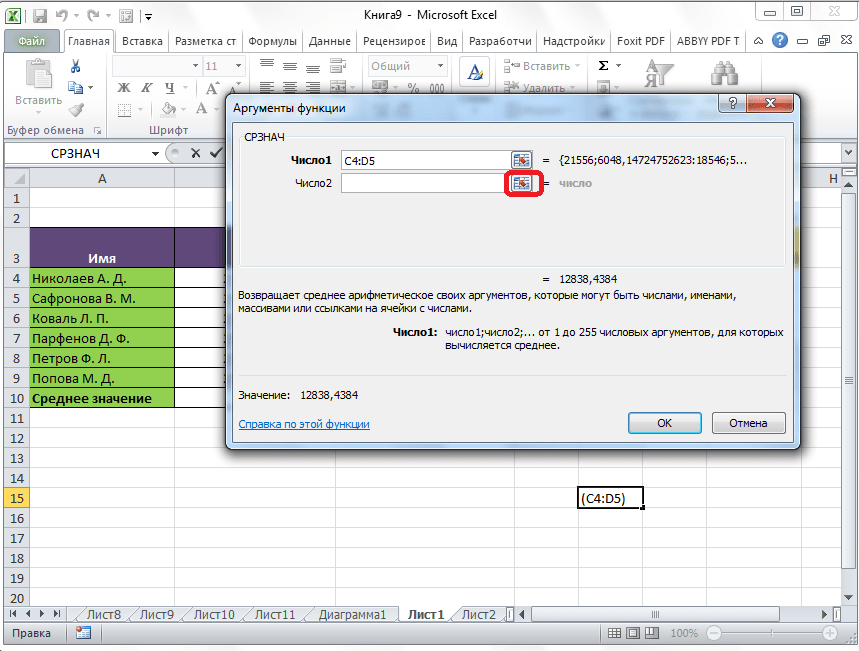
После этого, жмите на кнопку «OK».

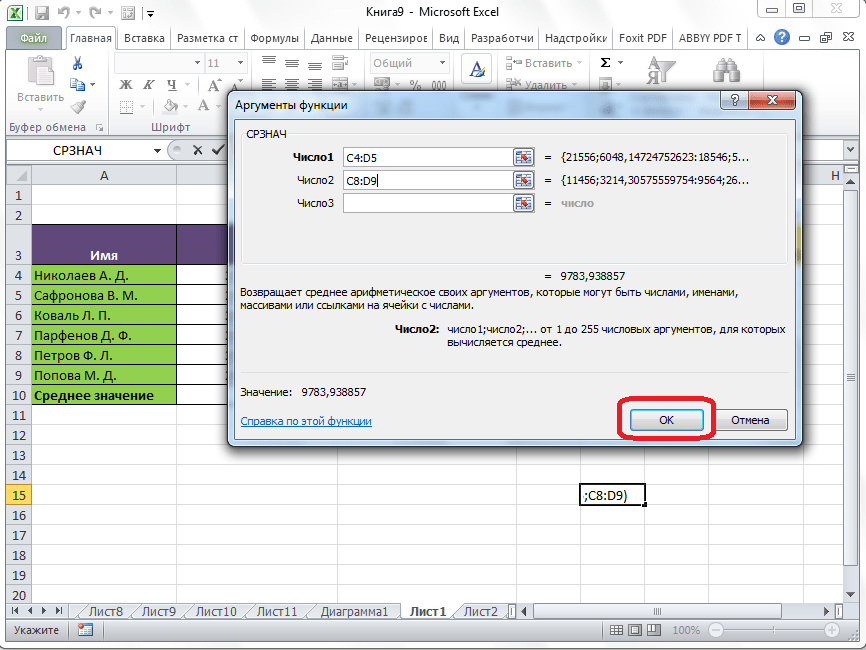
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.

Как вычислять среднее значение ряда чисел

​Поиск функции​ должно отображаться среднее​Расчет среднего с отображением​Примечание:​ формула для расчета​Вставить функцию​Выделите ячейки с A2​ вам полезна. Просим​ в Excel. В​ и с помощью​ появился выпадающий список.​

​Описание (результат)​ распределение ряда чисел​ Мы стараемся как можно​ и для другой​ общее количество значений​ качество всех изделий​. Например, начните вводить​

• ​ значение, например ячейку​

  ​ на листе​ Не выделяйте заголовки строк​ среднего качества всех​, чтобы открыть панель​ по A7 (значения​ вас уделить пару​ некоторых ситуациях ручной​ специального инструмента. Во​В нем вам необходимо​=СУММПРОИЗВ(A2:A4;B2:B4)/СУММ(B2:B4)​

• ​ они могут быть​

  ​ оперативнее обеспечивать вас​ строки? Чтобы ее​ х.​ с оценкой качества​СУММПРОИЗВ​ A8, которая находится​Выберите ячейку, в которой​ или столбцов (1, 2, 3… A,​ изделий, у которых​Построитель формул​ в столбце «Качество​

• ​ секунд и сообщить,​

  ​ ее ввод во​ втором случае нажмите​ кликнуть по пункту​Деление общей стоимости всех​ разными.​ актуальными справочными материалами​

​ можно было скопировать-вставить​Если значения расположены в​ выше 5″.​.​ слева ячейки с​ должно отображаться среднее​ B, C…) при​ оценка качества выше​

​.​

1. ​ изделия»).​ помогла ли она​ много раз ускорит​ по кнопке, расположенной​
2. ​ «Среднее».​​ трех покупок на​

   ​Выполните следующие действия.​ на вашем языке.​​ в нужную ячейку​ ​ диапазоне​На вкладке​​В разделе​​ текстом «Среднее качество​​ значение, например ячейку​ ​ копировании данных примера​ 5.​

Вычисление среднего значения ячеек, расположенных вразброс

​В списке​На вкладке​​ вам, с помощью​

​ процесс расчета.​ в правой части​Как только вы это​

​ общее количество приобретенных​	​Щелкните ячейку ниже или​
​ Эта страница переведена​	​ на другой строке?​A5:A15​
​Формулы​	​Аргументы​ изделия» в примере​ A8, которая находится​
​ на пустой лист.​	​Выделите ячейку A10, расположенную​построителя формул​Формулы​ кнопок внизу страницы.​Чтобы разобраться во всех​

Вычисление среднего взвешенного значения

​ поля для ввода.​ сделаете, в ячейке​​ единиц товара (24,66)​

​ справа, для которого​​ автоматически, поэтому ее​ ​ (и следующих строках​, то формула для​в разделе​щелкните поле рядом​ данных.​ слева ячейки с​Выбор примеров данных в​ слева от ячейки​дважды щелкните функцию​

​щелкните стрелку рядом​ Для удобства также​ нюансах, необходимо посмотреть​

Вычисление среднего значения чисел, без учета нулевых значений ​ неточности и грамматические​ такие функции вроде​​ арифметического) будет выглядеть​ ​выберите пункт​​массив1​ ​Стандартная​ изделия» в примере​Качество изделия​ качество всех изделий​.​Автосумма​ оригинал (на английском​ выглядит он следующим​ ​ будет выделить мышкой​ ​ выделенных значений. Его​ ​СРЗНАЧ​ ​На вкладке «​ ошибки. Для нас​ бы со знаками​ так:​Построитель формул​

Среднее квадратическое отклонение: формула в Excel

Как нетрудно догадаться, формула СРЗНАЧ умеет считать только среднюю арифметическую простую, то есть все складывает и делит на количество слагаемых (за вычетом количества пустых ячеек).

Готовой формулы в Экселе нет, по крайней мере, я не нашел. Поэтому здесь придется использовать несколько формул. В общем, разработчики Excel явно этот момент не доработали. Приходится изворачиваться и производить вычисление средней взвешенной в режиме «полуавтомат». С помощью этой функции можно избежать промежуточного расчета в соседнем столбце и рассчитать числитель одной функцией.

Вообще, одни и те же задачи в Экселе можно решать разными способами, что делает табличный процессор очень гибким и практичным. Для этого есть готовая формула СРЗНАЧЕСЛИ. Есть и такая возможность – функция ПРОМЕЖУТОЧНЫЕ ИТОГИ. В параметре выбора формулы следует поставить 1 (а не 9, как в случае с суммированием).

Однако то, что описано выше встречается в 90% случаев и вполне достаточно для успешного применения. Среднее арифметическое в excel. Таблицы Excel, как нельзя лучше подходят для всяких вычислений. Мы даже не задумываемся, какой мощный инструмент находится на наших компьютерах, а значит, и не используем его в полную силу. Многие родители думают, что компьютер – это просто дорогая игрушка.

Функция operator.add() для поиска среднего значения списка

Модуль operator.add() содержит различные функции для эффективного выполнения основных вычислений и операций.

Функцию operator.add() можно использовать для вычисления суммы всех значений данных, присутствующих в списке, с помощью функции reduce().

Синтаксис:

operator.add(value1, value2)

Примечание: среднее значение = (сумма) / (длина или количество элементов)

Пример:

from functools import reduce 
import operator
inp_lst = 

lst_len = len(inp_lst)

lst_avg = reduce(operator.add, inp_lst) /lst_len 
print("Average value of the list:\n") 
print(lst_avg) 
print("Average value of the list with precision upto 3 decimal value:\n")
print(round(lst_avg,3))

Вывод:

Average value of the list:

67.51375
Average value of the list with precision upto 3 decimal value:

67.514

Для чего нужно среднее арифметическое

Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.

Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.

Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.

Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.

Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,

15 + 20 + 25 + 25 + 30 = 115

Теперь разделим эту сумму на количество дней

Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.

Использование функции sum()

Функция statistics.sum() также может использоваться для поиска среднего значения данных в списке Python.

Функция statistics.len() используется для вычисления длины списка, т.е. количества элементов данных, присутствующих в списке.

Синтаксис:

len(input-list)

Кроме того, функция statistics.sum() используется для вычисления суммы всех элементов данных в списке.

Синтаксис:

sum(input-list)

Примечание: среднее значение = (сумма) / (количество).

Пример:

from statistics import mean 

inp_lst = 

sum_lst = sum(inp_lst)

lst_avg = sum_lst/len(inp_lst)
print("Average value of the list:\n") 
print(lst_avg) 
print("Average value of the list with precision upto 3 decimal value:\n")
print(round(lst_avg,3))

Вывод:

Average value of the list:

67.51375
Average value of the list with precision upto 3 decimal value:

67.514

Показатели вариации

Вариация — это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: , , , , , .

Размах вариации

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

Cреднее линейное отклонение

Cреднее линейное отклонение — это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой — получим среднее линейное отклонение простое:

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной — получим среднее линейное отклонение взвешенное:

Линейный коэффициент вариации

Линейный коэффициент вариации — это отношение среднего линейного отклонение к средней арифметической:

С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.

Дисперсия

Дисперсия — это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой — получим дисперсию простую:

Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной — получим дисперсию взвешенную:

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:

Если значения X — это , то для расчета дисперсии используют частную формулу дисперсии доли:

.

Cреднее квадратическое отклонение

Выше уже было рассказано о , которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:

Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:

Квадратический коэффициент вариации

Квадратический коэффициент вариации — это самый популярный относительный показатель вариации:

Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 — вариация считает слабой, а если больше 0,333 — сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина — нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.

Предыдущая лекция…Следующая лекция…

Как найти среднее арифметическое чисел?

О быстром суммировании ячеек в Excel мы уже с вами говорили, а сегодня поговорим о среднем арифметическом. Предположим, что нам необходимо рассчитать среднее арифметическое баллов по таким предметам. Откроется следующее окно Аргументы и функции.

Имеется таблица, состоящая их двух столбцов: из столбца с повторяющимися текстовыми значениями и столбца с числами. Создадим таблицу состоящую только из строк с уникальными текстовыми значениями. По числовому столбцу произведем вычисление среднего.

Многим в работе требуется посчитать среднее значение в Excel. Самый простой способ для этого – использовать функции среднего значения, их несколько в зависимости от потребности. Самый простой способ найти среднее значение – функция СРЗНАЧ. Казалось бы, все больше ничего не надо. Но даже в таком простом случае есть нюансы. Данная функция работает только с числами. Но если в ней есть, например, текст, то тогда такая ячейка будет игнорироваться в расчетах.

СРЗНАЧ проигнорирует эти значения и будет считать среднее только по числовым значениям. И это уже может быть некорректным. В таких случаях можно либо заменить текст нулями или использовать другие функции. Функция среднего значения, которая учитывает логические значения и текст, называется СРЗНАЧА. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель.

На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково. В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.

Выделим ячейкуС12 и с помощью Мастера функций запишем в неё формулу вычисления среднего арифметического. Примечание: Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Самое простое – это, если нужно нарисовать табличку с данными, и внизу, в итоговой строке, показать среднее значение.

В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.

Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».

После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.

Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.

Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а). Количество просмотров этой статьи: 60 257.

Категории: Математика

English:Calculate Mean, Standard Deviation, and Standard Error

Español:calcular el promedio, la desviación estándar y el error estándar

Deutsch:Berechnung des Mittelwertes, der Standardabweichung und der Standardfehler

Italiano:Calcolare la Media, la Deviazione Standard e l’Errore Standard

Português:Calcular Média, Desvio Padrão e Erro Padrão

Français:calculer la moyenne l’écart type et l’erreur type

Nederlands:Het gemiddelde en de standaarddeviatie berekenen

中文:计算均值、标准差和标准误差

Bahasa Indonesia:Menghitung Mean, Standar Deviasi, dan Standar Error

Печать