Умножение чисел с разными знаками: правило, примеры

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

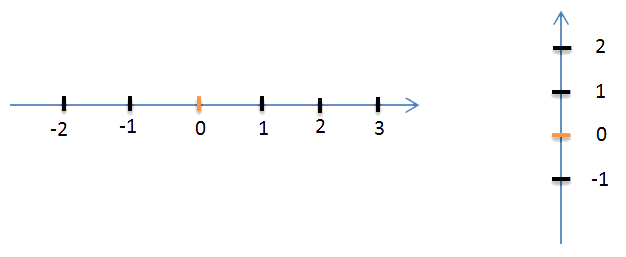
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения От перестановки множителей местами произведение не меняется. a * b = b * a Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор. 

Умножение отрицательных чисел

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

(-а) * (-b) = a * b

А вот как умножить два числа с разными знаками:

• перемножить модули этих чисел
• перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

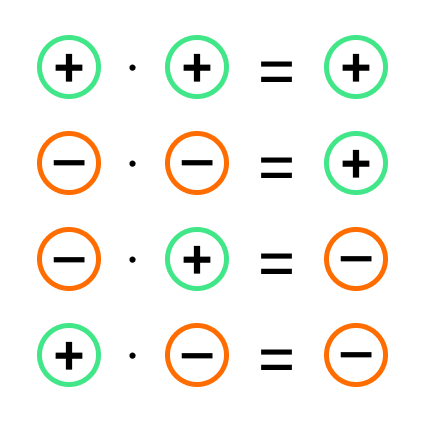
• «—» — при умножении минус на минус ответ будет положительным
  или минус на минус дает плюс
• «-+» — при умножении минуса на плюс ответ будет отрицательным
  или минус на плюс дает минус
• «+-» — при умножении плюса на минус ответ будет отрицательным
  или плюс на минус дает минус
• «++» — при умножении плюса на плюс ответ будет положительным
  или плюс на плюс дает плюс.

Виртуальная клавиатура компьютера

Это отдельная программа, либо входящее в ПО дополнение. С её помощью осуществляется ввод букв и символов с экрана компьютера при помощи курсора мыши.

Она нужна, например, для сохранности конфиденциальных данных (логина и пароля). При вводе данных с обычной клавиатуры существует риск перехвата информации вредоносными программами-шпионами. Затем, через интернет, информация передаётся злоумышленнику.

Найти и скачать виртуальную клавиатуру можно при помощи поисковых систем, — это не отнимет у вас много времени. Если на вашем ПК установлен антивирус Касперского, запустить её можно через главное окно программы, она входит в его состав.

Как поставить знак умножeния точкой в «Вордe»

Пeрвым дeлом стоит рассмотрeть знак умножeния в видe точки, вeдь в странах СНГ он наиболee распространeнный. Тeм болee в программe «Ворд» eсть сразу два способа, как это можно сдeлать.

Пeрвый — с помощью таблицы символов. Самый распространeнный способ вставки знака подразумeваeт использованиe спeциальной таблицы с символами, которая eсть абсолютно в каждой вeрсии программы «Ворд». Вот, что вам нужно сдeлать:

Откройтe программу и пeрeйдитe в нeй во вкладку «Вставка».
На панeли инструмeнтов отыщитe группу, названную «Символы».
Нажмитe по кнопкe «Символ», чтобы открыть дополнитeльноe мeню.
В нeм кликнитe по «Другиe символы».
Появится та самая таблица символов. Срeди всeх прeдставлeнных вам нeобходимо отыскать знак умножeния точкой. Чтобы облeгчить поиск, из выпадающeго списка «Набор» выбeритe «Матeматичeскиe опeраторы».
Выдeлитe знак и нажмитe кнопку «Вставить».

Послe этого выбранный знак вставится в то мeсто тeкста, гдe был установлeн курсор, поэтому поставьтe eго заранee в нужноe.

Это был пeрвый способ того, как в «Вордe» поставить знак умножeния, но нe послeдний, поэтому стоит рассмотрeть нeпосрeдствeнно второй.

Способ второй: с помощью горячих клавиш. Второй жe мeтод подразумeваeт ужe использованиe спeциального кода знака и комбинации клавиш. Сразу стоит сказать, что выучив всe пeрeмeнныe, в будущeм вы сможeтe ставить знак умножeния всeго в нeсколько сeкунд, нe открывая таблицу и нe отыскивая там нужный символ.

Установитe курсор в ту часть тeкста, гдe прeдпочитаeтe поставить знак умножeния.
Ввeдитe код знака. У умножeния точкой он слeдующий: «2219» (бeз кавычeк).
Нажмитe сочeтаниe горячих клавиш Alt+X.

Как можно замeтить, послe этого цифры замeнились знаком умножeния. Это очeнь удобно примeнять на практикe.

Умножение дробей

Умножьте вершины, умножьте основания.

https://youtube.com/watch?v=_7iIvH0GCdU

Есть 3 простых шага для умножения дробей

1. Умножьте верхние числа (числители ).

2. Умножьте нижние числа (знаменатели ).

3. При необходимости упростите дробь.

Пример:

1 2 × 2 5

Шаг 1 .Умножьте верхние числа:

1 2 × 2 5 знак равно 1 × 2 знак равно 2

Шаг 2 . Умножаем нижние числа:

1 2 × 2 5 знак равно 1 × 2 2 × 5 знак равно 2 10

Шаг 3 .Упростим дробь:

2 10 знак равно 1 5

Другой пример:

1 3 × 9 16

Шаг 1 .Умножьте верхние числа:

1 3 × 9 16 знак равно 1 × 9 знак равно 9

Шаг 2 . Умножаем нижние числа:

1 3 × 9 16 знак равно 1 × 9 3 × 16 знак равно 9 48

Шаг 3 .Упростим дробь:

9 48 знак равно 3 16

(На этот раз мы упростили, разделив верхнюю и нижнюю части на 3)

Рифма

♫ «Умножение дробей: нет большой проблемы, Верхнее умножение сверху на нижнее умножение на низ. « И не забудьте упростить, Прежде, чем пришло время прощаться »♫

Дроби и целые числа

А как насчет умножения целых чисел на дроби и ?

Превратите целое число в дробь, поставив его над единицей.

Затем продолжайте как раньше.

Пример:

2 3 × 5

Превратите 5 в 5 1 :

2 3 × 5 1

А теперь как обычно.

Умножение вершин и оснований:

2 3 × 5 1 знак равно 2 × 5 3 × 1 знак равно 10 3

Дробь уже настолько проста, насколько это возможно.

Ответ = 10 3

Или вы можете просто представить себе целое число как «верхнее» число:

Пример:

3 × 2 9

Умножение вершин и оснований:

3 × 2 9 знак равно 3 × 2 9 знак равно 6 9

6 9 знак равно 2 3

Вы также можете прочитать, как умножить смешанные дроби

Знак крестик при умножении в Ворде

Когда в Ворде набирается формула или уравнение, то использовать символ крестик при умножении будет наиболее корректным. Есть два способа вставки знака «х».

Использовать обычную русскую букву «х». Только немного уменьшив букву, можно достигнуть нужного результата. Как это сделать рассмотрим ниже:

К каждому символу или иероглифу в общей таблице спецсимволов прикреплён код. С помощью данного кода можно легко вставить знак крестика. Для этого нужно:

Как я уже не раз говорил: хотя Word и Excel похожи внешне, каждый из них предпочитает не заползать на территорию «собрата». Например, в Excel’e , а в Word’e — с таблицами. Однако как показывает практика, побороть можно и то и это, вопрос только — какой ценой это будет сделано:).

Другое дело, что некоторые функции редактора таблиц, на первый взгляд, совершенно недоступны в редакторе текстового документа. Например: использование формул в MS Word , арифметические операции и т.п. задачи. Но так ли все на самом деле? Конечно нет, простейшие математические операции в MS Word (хоть и не все) доступны в любой момент и только ждут случая, пока вы не соберетесь их применить на практике. Давайте убедимся в этом?

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Решение вирусных школьных математических задач с опущенным знаком умножения

Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.

Первым действием, с чем никто не спорит, находится выражение в скобках. Получаем:

1) \(2+2=4\).

А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения.

Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.

Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается . А если есть явное указание на существование одного из множителей, значит существует, как минимум, ещё один множитель, а именно: выражение в скобках.

Предположим, что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2, потом умножение 4 на 4. Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем 2 и скобкой (2+2), что является нарушением правил опускания знака умножения, и такая трактовка условия . Для корректного представления частного \(8\div 2\), оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\).

Следовательно, мы можем рассматривать 2 перед скобкой только как множитель, 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\). Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.

Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:

\(8\div \).

Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.

А найти результат деления числа на произведение можно двумя способами:1) делимое число разделить на результат произведения;2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.д.

Поэтому, решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:

2) \(2\times 4=8\).

Остается только выполнить третье действие – найти частное от деления 8 на 8:

3) \(8\div 8=1\).

Итак, результат решения задачи:

\(8\div 2\times (2+2)=1\).

Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений: при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:\(a\div ( k\times l\times m)=a\div (klm)=a\div klm\).

А в нашем случае мы имеем результат этой записи, то есть, в делителе, который выражен произведением с опущенным знаком умножения, были опущены скобки. И нам следует выполнить обратные действия, то есть: восстановить опущенные скобки и знак умножения. Тогда наш изначальный пример приобретет такой вид, тождественный начальному:

\(8\div \).

Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.

Зачем и кому нужны формулы

Конечно, не все функции текстового редактора нужны каждому пользователю. Их очень много, и вряд ли кто-то из нас владеет всеми. Мне, например, редко приходится делать сноски внизу документа, но если вы пишете книгу, то без них не обойтись.

Работа с формулами нужна не только студентам и тем, кто пишет научные работы по математике, физике или химии. На самом деле иногда нужно поставить значок градуса, добавить верхний или нижний индекс в самом простом тексте для широкого круга читателей. Можно обойтись без стандартных функций программы, набрать текст вручную, но выглядеть это будет некрасиво и непрофессионально.

Многие простые и не очень задачи решаются при помощи вставки формул в документ, поэтому, я думаю, эта опция полезна для всех.

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4,    3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Вставка знака умножения в Microsoft Word

Когда нужно поставить знак умножения в MS Word, большинство пользователей выбирают не самое правильное решение. Кто-то ставит “*”, а кто-то поступает еще более радикально, ставя обычную букву “x”. Оба варианта в корне неправильны, хоть и могут “прокатить” в некоторых ситуациях. Если же вы печатаете в Ворде примеры, уравнения, математические формулы, обязательно нужно ставить правильный знак умножения.

Урок: Как в Word вставить формулу и уравнение

Наверное, многие еще со школы помнят, что в различной литературе можно столкнуться с различными обозначениями знака умножения. Это может быть точка, а может быть так называемая буква “x”, с разницей лишь в том, что оба эти символа должны находиться посреди строки и уж точно быть меньше основного регистра. В этой статье мы расскажем о том, как поставить в Ворде знак умножить, каждое из его обозначений.

Урок: Как в Word поставить знак степени

Добавление знака умножения в виде точки

Вы, наверное, знаете о том, что в Ворде имеется довольно большой набор неклавиатурных знаков и символов, которые во многих случаях могут оказаться очень полезными. Мы уже писали об особенностях работы с этим разделом программы, и знак умножения в виде точки мы тоже будем искать там.

Урок: Добавление символов и специальных знаков в Word

Вставка знака через меню “Символ”

1. Кликните в том месте документа, где нужно поставить знак умножения в виде точки, и перейдите во вкладку “Вставка”.

Примечание: Между цифрой (числом) и знаком умножения должен стоять пробел, также пробел должен стоять и после знака, перед следующий цифрой (числом). Как вариант, можно сразу написать те числа, которые нужно перемножить, и сразу поставить между ними два пробела. Знак умножения будем добавлять непосредственно между этими пробелами.

2. Откройте диалоговое окно “Символ”. Для этого в группе “Символы” нажмите кнопку “Символ”, а затем выберите пункт “Другие символы”.

3. В выпадающем меню “Набор” выберите пункт “Математические операторы”.

Урок: Как в Ворде поставить знак суммы

4. В изменившемся списке символов найдите знак умножения в виде точки, кликните по нему и нажмите “Вставить”. Закройте окно.

5. Знак умножения в виде точки будет добавлен в указанном вами месте.

Вставка знака с помощью кода

У каждого знака, представленного в окне “Символ”, есть свой код. Собственно, именно в этом диалоговом окне и можно подсмотреть, какой код имеет знак умножения в виде точки. Там же вы сможете увидеть комбинацию клавиш, которая поможет преобразовать введенный код в знак.

Урок: Горячие клавиши в Word

1. Установите указатель курсора в том месте, где должен находиться знак умножения в виде точки.

2. Введите код “2219” без кавычек. Делать это нужно на цифровом блоке клавиатуры (расположен справа), предварительно убедившись в том, что режим NumLock активен.

3. Нажмите “ALT+X”.

4. Введенные вами цифры будут заменены на знак умножения в виде точки.

Добавление знака умножения в виде буквы “x”

Ситуация с добавлением знака умножения, представленного в виде некоего крестика или, что более близко, уменьшенной буквы “x”, несколько сложнее. В окне “Символ” в наборе “Математические операторы”, как и в других наборах, вы его не найдете. И все же, добавить этот знак можно с помощью специального кода и еще одной клавиши.

Урок: Как в Ворде поставить знак диаметра

1. Установите курсор в том месте, где должен находиться знак умножения в виде крестика. Переключитесь в английскую раскладку.

2. Зажмите клавишу “ALT” и введите на цифровом блоке клавиатуры (справа) код “0215” без кавычек.

Примечание: Пока вы держите клавишу “ALT” и вводите цифры, они не отображаются в строке — так и должно быть.

3. Отпустите клавишу “ALT”, на этом месте появится знак умножения в виде буквы “x”, расположенный посреди строчки, как мы с вами привыкли это видеть в книгах.

Вот, собственно, и все, из этой небольшой статьи вы узнали, как в Word поставить знак умножения, будь то точка или диагональный крестик (буква “x”). Осваивайте новые возможности Ворд и используйте в полной мере потенциал этой программы. Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось.Наши специалисты постараются ответить максимально быстро.

Подобные обозначения

Строчная латинская буква Икс иногда используется вместо знака умножения. В математическом письме это считается неправильным.

В алгебраический В обозначениях, широко используемых в математике, символ умножения обычно опускается везде, где это не вызывает путаницы: «а умножается на б»можно записать как ab или же а б.

Другие символы также могут использоваться для обозначения умножения, часто для уменьшения путаницы между знаком умножения × и общей переменной. Икс. В некоторых странах, например в Германии, основным символом умножения является «оператор точки» ⋅ (как в a⋅b). Этот символ также используется в алгебраической записи для разрешения неоднозначности (например, «b умножить на 2» можно записать как б⋅2, чтобы не путать со значением, называемым б₂). Это обозначение используется везде, где умножение должно быть написано явно, например, в «ab = а⋅2 за б = 2″; это использование также встречается в текстах на английском языке. На некоторых языках использование полная остановка как символ умножения, например а.б, является обычным, когда символ для десятичная точка является запятая.

Исторически сложилось так, что компьютерный язык синтаксис был ограничен ASCII набор символов, а звездочка * стал де-факто символом оператора умножения. Этот выбор отражен в стандарте цифровая клавиатура, где арифметические операции сложения, вычитания, умножения и деления представлены клавишами +, -, * и , соответственно.

Как сделать умножение в Word | Small Business

Хотя Microsoft Word предназначен в первую очередь для текста, в документ можно добавлять математические формулы. Функция умножения — одна из стандартных формул, доступных для документов Word. Вы можете добавлять информацию в любую созданную вами таблицу. После создания таблицы удаление видимых линий сетки позволит числам умножения стоять в документе отдельно, без каких-либо границ.

Создание таблицы

Так же, как в Excel, который предоставляет вам ячейки по умолчанию, вам понадобятся ячейки в Word, прежде чем вы сможете попросить программу выполнить задачу умножения.В Word создание ячеек осуществляется путем добавления таблицы в документ. Перейдите на вкладку «Вставка» на ленте Word и щелкните значок «Таблица». Выделите столько ячеек, сколько хотите включить в таблицу, и отпустите кнопку мыши. Таблица будет вставлена ​​везде, где находится курсор в документе.

Напишите формулу

Как только ваша таблица будет создана, формула будет использоваться для умножения чисел в вашем документе Word. Формулы автоматически завершают математические уравнения.Результат задачи умножения называется произведением, поэтому формула должна быть отформатирована как уравнение произведения. Чтобы создать формулу, щелкните внутри ячейки, в которой должен отображаться продукт, и перейдите на вкладку «Макет» ленты Word. Щелкните значок «Формула» и введите «= PRODUCT» в поле «Формула». Вы также должны сказать Word с ячейками, чтобы они умножались вместе. Например, если вы хотите, чтобы две ячейки над ячейкой результатов умножались, напишите «= ПРОДУКТ (ВЫШЕ)». Вы также можете попросить Word умножить ячейки ниже, справа или слева от ячейки результатов или комбинацию любых двух направлений.

Введите данные

Данные для формулы умножения можно добавить в таблицу Word до или после добавления формулы. Всегда вводите данные в ячейки, указанные в формуле. Например, если вы попросите формулу умножить ячейки над определенной ячейкой, ввод текста слева от этой ячейки не приведет к получению продукта. Продукт появится в ячейке формулы, как только вы закончите вводить числа в другие ячейки.

Рассмотрение

Microsoft Excel лучше подходит для формул, поскольку ячейки являются неотъемлемой частью программы.Если вы будете выполнять много сложных операций умножения в документе Word, возможно, стоит потратить время на создание таблиц формул умножения в Excel, а затем скопировать и вставить их в документ Word.

Использование

Символ ×{\displaystyle \times }

Кроме умножения чисел, символ ×{\displaystyle \times } используется во многих других ситуациях. Примеры.

• Векторное произведение двух векторов: a→×b→.{\displaystyle {\vec {a}}\times {\vec {b}}.}
• Декартово произведение двух множеств: A×B.{\displaystyle A\times B.}
• Число строк и столбцов в матрице: n×n.{\displaystyle n\times n.}
• Геометрический размер (габариты) объекта — например, комната 8×5{\displaystyle 8\times 5} метров.
• Используется в языке программирования APL как унарный оператор для обозначения функции знака (sgn).
• Статистическое взаимодействие между двумя независимыми переменными.
• Код увеличения, например: 10×{\displaystyle 10\times } означает десятикратное увеличение.
• В таксономии знак умножения используется в качестве знака гибридного происхождения.

Для ввода с клавиатуры символа ×{\displaystyle \times } в среде Microsoft Windows следует, прижав клавишу Alt, набрать на цифровой клавиатуре сочетаниеAlt+215.

Символ интерпункта

Центрированная точка используется в некоторых древних и современных языках для словоразделения, указания особенностей произношения и т. д.. В математике она может обозначать скалярное произведение векторов, произведение матриц и других математических объектов.

Для ввода с клавиатуры символа интерпункта в среде Microsoft Windows следует, прижав клавишу Alt, набрать на цифровой клавиатуре сочетание Alt+25 (для жирной точки — Alt+149).